在学习SVM模型时,看到了拉格朗日乘子,顺便回顾一下KKT条件。
争取用最简单直白的方式来解释KKT条件。
0.1. 首先,KKT条件定义
对于极小化问题
这里所有函数都可以不是线性的,约束条件里面有等式约束和不等式约束,看起来比较复杂。
先扔出来KKT条件是什么:
满足KKT条件的解,是极值点的必要条件。
0.2. 无约束情形
$\min f(x)$直接求这个函数的极小值$~\bigtriangledown f = 0~$即可。在图上画等值线,在某个点达到极小值。
0.3. 仅等式约束情形
假设只有一个等式约束函数$h(x)=0$,等式约束使得,$f(x)$的极值点,在等值线与$h(x)$相切的地方达到。
相切的地方,$f(x)$和$h(x)$的梯度在同一条直线上,因此$\bigtriangledown f(x) + \lambda\bigtriangledown h(x) = 0$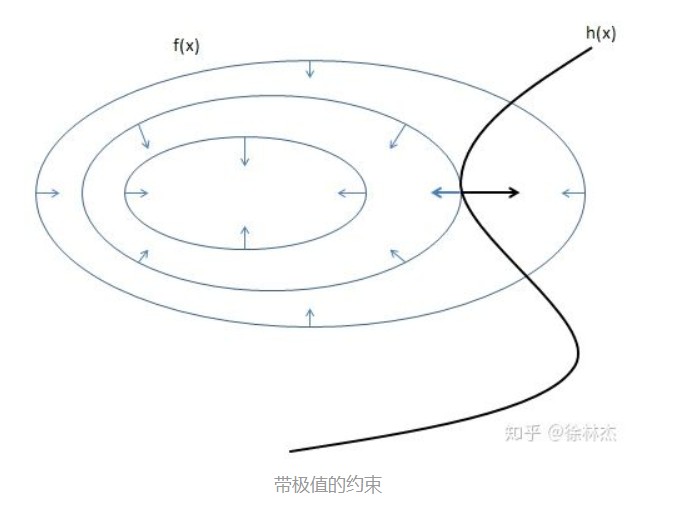
多等式约束:
多个等式约束时,$\bigtriangledown f(x)$在$\bigtriangledown h_1(x)$和$\bigtriangledown h_2(x)$张成的空间中,所以$\bigtriangledown f(x) + \lambda_1\bigtriangledown h_1(x) + \lambda_1\bigtriangledown h_2(x) = 0$.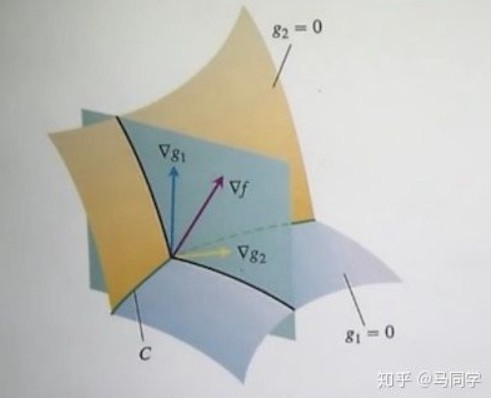
想象该图的目标函数是一个球体,最小值应在球心处达到,然后在球上被$g_1$和$g_2$俩函数切了两刀,最小值只能在两刀相交的一条线$C$上达到了。切线上$f(x)$的梯度方向确实是$g_1$和$g_2$的线性组合。
当只有等式约束时,只需求解方程组:
从拉格朗日乘子法的角度也可以推出以上这个方程组:将等式约束写入目标函数,变成无约束问题,并且令新的目标函数为$~L(x,\lambda) = f(x) + \sum\limits_i\lambda_i h_i(x)$,然后对$x$、$\lambda$求偏导,即得到上面的方程组。这里$\lambda$称为拉格朗日乘子。
0.4. 不等式约束情形
先考虑一个简单情形,目标函数是同心圆$~\min f(x_1, x_2) = x_1^2 + x_2^2~$. 无约束时极值点在原点(0,0)达到。如果有约束:
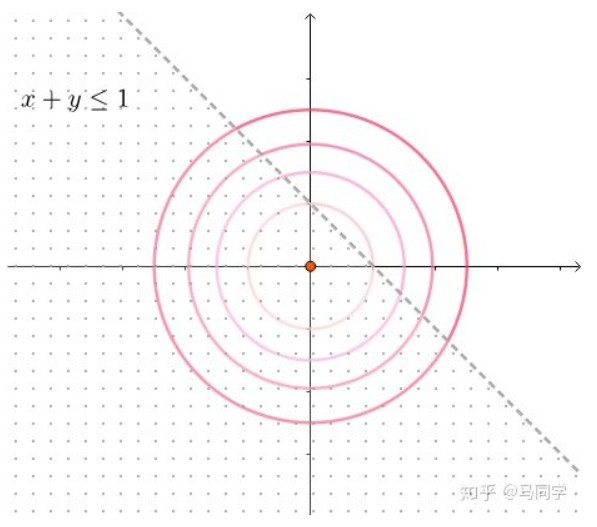
从图上可以看出,不等式约束经过原点(极值点)。这时这个约束没有起作用,极值点依然只需求解$f$的导数而得到。
另一种情况就是不等式约束起作用,如果有约束:
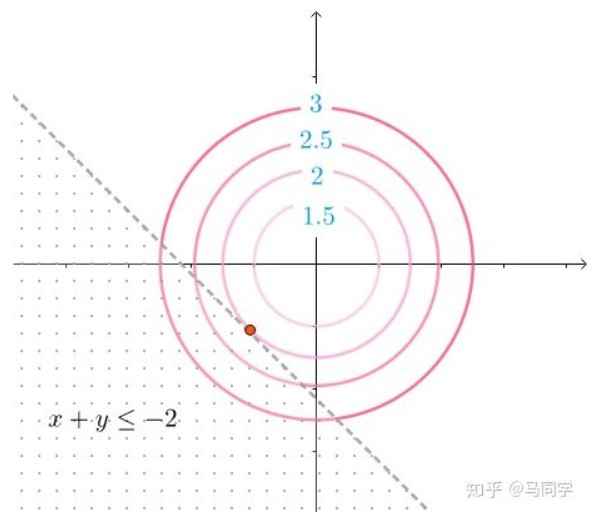
从图上可以看出,这个不等式起作用了,使得目标函数最小值在不等式边缘相切处达到。这时,跟等式约束$~h_2(x_1, x_2) = x_1 + x_2 + 2 = 0~$一样效果。
在切点处,$f~$和$~h_2~$共线,又因为$f~$的梯度方向$~\bigtriangledown f~$跟$~h_2~$的梯度方向$~\bigtriangledown h_2~$相反,所以有$~\bigtriangledown f + \mu\bigtriangledown h = 0, \mu>0~$.
总结:当不等式不起作用时,相当于$\mu=0$,当不等式起作用时,$g(x) = 0$。
当只有等式约束时,只需求解方程组:
0.5. 综合情形
再放一遍KKT条件,加深一下印象!
通俗来说,不等式约束中,只有起作用的约束条件,拉格朗日乘子才$\mu\neq$0.
杨一宸的Comments:
KKT就是下降不可行,可行不下降;
按线性规划对偶的理解,就是可行方向锥里的任意向量和目标函数梯度方向的内积小于0
参考资料: