本文主要介绍拉格朗日对偶与SVM的关系，以及为什么要用对偶来解决

1. 拉格朗日对偶

1.1. Primal问题

考虑极小化问题

$\begin{array}{ll} \text{min} & f(w) \\ \text{s.t.} & g_j(w) \le 0, ~~j= 1,\dots, k\\ & h_i(w) = 0, ~~i =1,\dots, l \end{array}$

对于基本的SVM模型，$f(x)=\frac{1}{2}||w||^2$，$g_j(w)=-y_i(w^Tx_i+b)+1\le 0$。

定义拉格朗日函数为： $\mathcal{L}(w,\alpha,\beta)=f(w)+\sum\limits_{i=1}^k\alpha_ig_i(w)+\sum\limits_{i=1}^l\beta_ih_i(w)$ ，将有约束问题变成无约束的。这里使用的拉格朗日乘子的符号跟上一篇文章的不一样，不过不影响阅读。

令 $\theta_P(w) = \max\limits_{\alpha\ge0,\beta}\mathcal{L}(w,\alpha,\beta)$ .我们发现，对于任意给定的$w$，如果$w$违反了约束条件（即$g_i(w)>0$或者$h_i(w)\neq0$），则存在某组拉格朗日乘子，使得$\theta_P(w)=\infty$；相反，如果$w$满足约束条件，$\theta_P(w)=f(w)$。因此，

$\theta_P(w)= \begin{cases} f(w), & \text{if w satisfies primal constraints} \\ \infty, & \text{otherwise} \end{cases}$

为什么 要构造$\theta_P(w)$

$\theta_P(w)$与原函数$f(w)$在$w$满足约束时取值相等，考虑极小化$\theta_P(w)$与极小化原问题等价；
同时，又构造出$\min\max$的形式，方便后面求拉格朗日对偶

因此，考虑极小化问题 $\min\limits_w\theta_P(w)=\min\limits_w\max\limits_{\alpha\ge0,\beta}\mathcal{L}(w,\alpha,\beta)$ ，与极小化原问题的解相同。

1.2. Dual问题

拉格朗日对偶（已经是无约束了），是将Primal问题的$\min$和$\max$互换，即可得到对偶问题$\max\limits_{\alpha\ge 0,\beta}\min\limits_w\mathcal{L}(w,\alpha,\beta)$，就这么简单嘎嘎。

Primal问题和Dual问题是有关联的：Primal问题的最优值，是大于等于对偶问题的最优值（弱对偶性）。即

$d^* = \max\limits_{\alpha\ge 0,\beta}\min\limits_w\mathcal{L}(w,\alpha,\beta) \le \min\limits_w\max\limits_{\alpha\ge0,\beta}\mathcal{L}(w,\alpha,\beta) = p^*$

在特定情况下（Slater条件，这里不详细解释），我们有 $d^* = p^*$ (强对偶性)。在满足Slater条件时，必存在一组 $w^*,\alpha^*,\beta^*$ ，使得

$w^*$ 是Primal问题的解，
$\alpha^*,\beta^*$ 是Dual问题的解，
并且 $p^*=d^*=\mathcal{L}(w^*,\alpha^*,\beta^*)$
$w^*, \alpha^*,\beta^*$ 满足KKT条件：

$\begin{array}{rl} \frac{\partial}{\partial w_i}\mathcal{L}(w^*,\alpha^*,\beta^*) = 0, & i =1,\dots, n \\ \frac{\partial}{\partial \beta_i}\mathcal{L}(w^*, \alpha^*, \beta^*) =0 , & i = 1,\dots, l \\ \alpha^*_i g_i(w^*) = 0, & i = 1, \dots,k \\ g_i(w^*)\le 0, & i = 1,\dots, k \\ \alpha^* \ge 0, & i = 1,\dots, k \end{array}$

另外，如果某组 $w^*, \alpha^*,\beta^*$ 满足KKT条件，则它也是原问题和对偶问题的解。

KKT条件的第三组等式称为松弛互补条件，当 $\alpha^*>0$ 时，有 $g_i(w^*)=0$ ，即该约束条件$g_i(w^*)\le 0$达到等号，是”起作用”的约束条件。

在SVM模型中，每个训练样本点都代表一个不等式约束，那些达到等号的不等式约束，就是到分割超平面记录严格等于1的点，就是支撑向量（support vector）。SVM模型只需要确定这少数的几个支撑向量（即等式约束，即$\alpha^*>0$的点）。

2. 对偶在SVM上的应用

2.1. 支撑向量

SVM的目标是找到最优的分割超平面，使得支撑向量到这个平面的距离最大，即能够最大程度的区分两类样本。假设总共有$m$个训练样本，每个样本有$n$个特征，目前$m, n$的大小关系不重要，后面会讨论什么时候更加适合使用对偶的思想。SVM的数学规划形式为：

$\begin{array}{rl} \min\limits_{w,b} & \frac{1}{2}||w||^2 \\ \text{s.t.} & y_i(w^Tx_i+b)\ge 1 , i=1,\dots,m \end{array}$

我们把模型的约束条件改写为$g_i(w)=-y_i(w^Tx_i+b)+1\le 0$，与前文的格式保持一致。每一个训练样本，都对应这样一个不等式约束$g(w)$。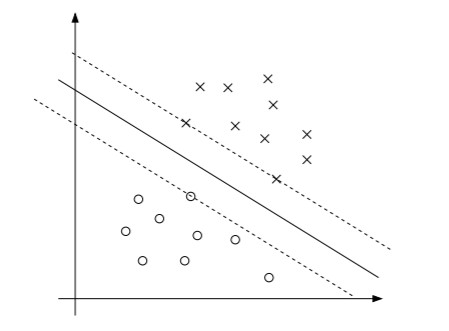
dual1

上图有三个支撑向量，这三个点的margin最小，这三个点对应的$g(w)=0$，也就是在最优解中，只有这三个点对应的$\alpha$可能大于0，其余点对应的$\alpha$都只能等于0（因为松弛互补条件）。一般的，支撑向量的数量比训练集合小很多。如果我们能找到一种计算方式，使得在做预测的时候，只需要考虑这几个支撑向量，那么这个问题将变得容易很多。

2.2. 对偶问题

我们来验证拉格朗日对偶能不能帮到我们：首先将原始SVM模型改写成无约束形式，

$\mathcal{L}(w,b,\alpha) = \frac{1}{2}||w||^2 - \sum\limits_{i=1}^m\alpha_i[y_i(w^Tx_i+b)-1].$

然后考虑它的对偶形式 $\max\limits_{\alpha\ge 0}\min\limits_{w,b}\mathcal{L}(w,b,\alpha)$ .先求内部的min，固定$\alpha$，求出$w,b$使得$\mathcal{L}(w,b,\alpha)$极小化，这个过程很简单，就是求$\frac{\partial}{\partial w}\mathcal{L}=0$，$\frac{\partial}{\partial b}\mathcal{L}=0$.

$\frac{\partial}{\partial w}\mathcal{L}(w,b,\alpha) = w - \sum\limits_{i=1}^m\alpha_iy_ix_i =0 ~~~\Rightarrow~~~ w = \sum\limits_{i=1}^m\alpha_iy_ix_i$ $\frac{\partial}{\partial b}\mathcal{L}(w,b,\alpha) = \sum\limits_{i=1}^m\alpha_iy_i=0$

把以上两个关系式带入拉格朗日函数，得到的是$\min\limits_{w,b}\mathcal{L}$的表达式

$\begin{array}{ll} \min\limits_{w,b}\mathcal{L}(w,b,\alpha) & = \frac{1}{2}(\sum\limits_{i=1}^m\alpha_iy_ix_i)^2 - \sum\limits_{i=1}^m\alpha_iy_ix_i(\sum\limits_{i=1}^m\alpha_iy_ix_i) - b\sum\limits_{i=1}^m\alpha_iy_i + \sum\limits_{i=1}^m\alpha_i\\ & = \sum\limits_{i=1}^m\alpha_i - \frac{1}{2}(\sum\limits_{i=1}^m\alpha_iy_ix_i)^2 \\ & = \sum\limits_{i=1}^m\alpha_i - \frac{1}{2}\sum\limits_{j,j=1}^my_iy_j\alpha_i\alpha_jx_i^Tx_j \end{array}$

现在把得到的 $\min\limits_{w,b}\mathcal{L}$ 的以上表达式，外面套上$\max\limits_{\alpha\ge 0}$，得到下面的规划：

$\begin{array}{rl} \max\limits_{\alpha} & \sum\limits_{i=1}^m\alpha_i - \frac{1}{2}\sum\limits_{j,j=1}^my_iy_j\alpha_i\alpha_jx_i^Tx_j \\ s.t. & \alpha_i\ge 0, i=1,\dots, m \\ & \sum\limits_{i=1}^m\alpha_iy_i = 0 \end{array}$

注意，这个规划的变量只有$\alpha$。因为SVM的规划符合强对偶性，所以有 $p^*=d^*$ ，因此我们可以通过求解SVM的对偶问题来解原问题。回忆我们之前讲的，只有支撑向量对应的$\alpha$才可能不为0，其他的全为0。所以对偶问题的解 $\alpha_i(i=1,\dots,m)$ ，一定满足大多数均为0，只有少数几个不为0. 后面通过SMO算法可以求解此对偶问题。求解出来 $\alpha_i$ 之后，可以通过$w = \sum\limits_{i=1}^m\alpha_iy_ix_i$ 进而求得$w^*$.再通过

$b^* = -\frac{\max\limits_{i:y_i=-1}w^{*T}x_i + \min\limits_{i:y_i=1}w^{*T}x_i }{2}$

求得$b^*$.

3. 灵魂拷问：为什么要用对偶？

（第一个核心点）让我们回头再看看等式$w = \sum\limits_{i=1}^m\alpha_iy_ix_i$，完全用$\alpha$来表示最优的参数$w$。假设我们已经通过训练确定了参数$w$和$b$，现在要预测一个新的样本点$x$，我们要计算的是$w^Tx+b$，并根据结果的正负来决定$y$取值为1还是0.
$\begin{array}{ll} w^Tx+b & = (\sum\limits_{i=1}^m\alpha_iy_ix_i)^Tx+b \\ & = \sum\limits_{i=1}^m\alpha_iy_i(x_i^Tx) +b \end{array}$
我们早已发现，除了那些支撑向量外，其余的点对应的$\alpha$均为0。所以上式的求和项中，许多项直接为0，我们只需要计算支撑向量跟$x$的乘积。所以通过对偶的方法，引入了$\alpha$，在做预测时，计算变得非常简便。
（第二个核心点）通过对偶，目标函数有$x_i^Tx_j$的形式，可以引入Kenel trick
原问题的拉格朗日函数 $\min\limits_{w,b}\max\limits_{\alpha\ge 0}\mathcal{L}(w,b,\alpha)$ ，内测求 $\theta = \max\limits_{\alpha\ge 0}\mathcal{L}$ 的部分，因为有约束条件 $\alpha\ge 0$ 的缘故，求极值点比较困难，因为 $\frac{\partial\theta}{\partial\alpha_i}=0$ 的 $\alpha$ 不一定在 $\alpha\ge 0$ 时达到。
但对偶问题先求$\min\limits_{w,b}\mathcal{L}$，$w,b$均没有限制，直接求偏导数等于0，得到一些关系式，带回拉格朗日函数消去$w,b$。然后再通过SMO算法来求解外侧的max部分。

4. 参考资料

重点参考Andrew Ng的Lecture notes

5. Open问题

如果从拉格朗日对偶来推导出KKT条件？目前的资料都是建立在强对偶的条件下，得到KKT。但KKT不一定要在强对偶时才能使用。