EM算法

EM算法解决带有隐变量的混合模型的参数估计（极大似然估计MLE），主要用来解决生成模型。只求X的概率可能会非常复杂，无法得到X的概率形式，这时假设它是一个生成模型，假定有隐变量Z，数据从$Z\rightarrow$X. 因此，X具有了新的形式$p(X) = \frac{p(X,Z)}{p(Z|X)}$.

一般的参数估计，比如MLE，$\theta_{MLE} = \arg\max_\limits{\theta}\log P(x|\theta)$，直接对$\theta$求导数，就可以直接得到解析解。但对于含有隐变量的混合模型（比如GMM），直接求得解析解非常困难。

EM是迭代的算法，

$$\theta^{(t+1)} = \arg\max\limits_{\theta}\int_z\log p(x,z|\theta)\cdot p(z|x, \theta^{(t)})dz = \arg\max\limits_{\theta}E_{z|x,\theta^{(t)}}[\log p(x,z|\theta)] \tag{1}$$

其中E步是写出期望这个表达式，M步求期望最大的$\theta^{(t+1)}$.

1. 算法收敛性

通过上式的不断迭代，$\theta^{(t)}\rightarrow\theta^{(t+1)}$，$\log p(x|\theta^{(t)})\le\log p(x|\theta^{(t+1)})$，这样log-likelihood一直在增加，最终算法收敛。

通项可写为：

$$\log p(x|\theta) = \log p(x,z|\theta) - \log p(z|x,\theta)\\$$

两边关于分布$p(z|x, \theta^{(t)}))$求积分（求期望）：

$$\begin{array}{rl} 左边&=\int_z p(z|x,\theta^{(t)})\cdot \log p(x|\theta) dz\\ &=\log p(x|\theta)\int_z p(z|x,\theta^{(t)})dz \\ &=\log p(x|\theta) \\ 右边&={\color{red}\int_z p(z|x,\theta^{(t)})\cdot \log p(x,z|\theta)dz} - {\color{blue}\int_z p(z|x,\theta^{(t)})\cdot\log p(z|x,\theta)dz} \\ & = \color{red}Q(\theta, \theta^{(t)}) - {\color{blue}H(\theta, \theta^{(t)})} \end{array}$$

其中$Q(\theta, \theta^{(t)})$就是$(1)$式的积分。又因为$\theta^{(t+1)}$的取值使得积分达到最大，有$Q(\theta^{(t+1)}, \theta^{(t)})\ge Q(\theta, \theta^{(t)})$，对任意$\theta$都成立。特别地，取$\theta=\theta^{(t)}$也同样成立，$Q(\theta^{(t+1)}, \theta^{(t)})\ge Q(\theta^{(t)}, \theta^{(t)})$. 只需证明$H(\theta^{(t+1)}, \theta^{(t)})\le H(\theta^{(t)}, \theta^{(t)})$，就可以得到结论$\log p(x|\theta^{(t)})\le\log p(x|\theta^{(t+1)})$.

$$\begin{array}{rl} &H(\theta^{(t+1)}, \theta^{(t)}) - H(\theta^{(t)}, \theta^{(t)})\\ = & \int_z p(z|x,\theta^{(t)})\cdot \log p(z|x,\theta^{(t+1)})dz - \int_z p(z|x,\theta^{(t)})\cdot \log p(z|x,\theta^{(t)})dz \\ = & \int_z p(z|x,\theta^{(t)})\cdot\log\frac{p(z|x,\theta^{(t+1)})}{p(z|x,\theta^{(t)})}dz\\ = & -KL(p(z|x,\theta^{(t)})~||~p(z|x,\theta^{(t+1)}))\\ \le & 0 \end{array}$$

2. ELBO + KL divergence

• E-step：写出log complete data关于后验概率分布的期望$p(z|x,\theta^{(t)}) \rightarrow E_{z|x,\theta^{(t)}}[\log p(x,z|\theta)]$
• M-step：选择$\theta$使得期望达到最大

通过这种方式，迭代地使得$\log p(x|\theta)$达到最大（收敛性已经证明）。虽然可以证明这个迭代公式确实可以使log-likelihood达到最大，但还没有解释这个迭代公式是怎么得到的。本节来推导出这个迭代公式。

从log-likelihood出发：

$$\begin{array}{rl} \log p(x|\theta) = & \log p(x,z|\theta) - \log p(z|x,\theta)\\ = & \log\frac{p(x,z|\theta)}{q(z)} - \log\frac{p(z|x,\theta)}{q(z)} \end{array}$$

等式两边关于$q(z)$求期望（积分）：

$$\begin{array}{rl} 左边 & = \int_z q(z)\cdot\log p(x|\theta)dz\\ & = \log p(x|\theta) \int_z q(z)dz\\ & = \log p(x|\theta)\\ 右边 & = {\color{red}\int_z q(z)\log\frac{p(x,z|\theta)}{q(z)}dz} ~{\color{blue} - \int_z q(z)\log\frac{p(z|x,\theta)}{q(z)}dz}\\ & = {\color{red}ELBO} + {\color{blue}KL(q(z)~||~p(z|x,\theta))} \end{array}$$

所以有$\log p(x|\theta) = ELBO + KL(q(z)~||~p(z|x,\theta))$，其中p是后验。ELBO是Evidence of Lower Bound的缩写，可看作是关于q的期望，同时ELBO可写成q和$\theta$的函数$L(q,\theta)$。因为KL divergence $\ge0$，所以$\log p(x|\theta)\ge ELBO$. 当且仅当$p=q$时，$\log p(x|\theta) = ELBO$.

2.1. EM算法的思路

在每一步迭代，让ELBO达到最大，如果ELBO能够持续增大，那么log-likelihood$~\log p(x|\theta)$就可以持续增大。

• E-step是固定参数$\theta$，调整q让ELBO达到最大。极大似然$p(x|\theta)$与$q(z)$的选择无关，$q(z)$在等于后验$p(z|x,\theta^{(t)})$时，能够使ELBO最大。也就是当KL divergence=0时，即$q(z) = p(z|x, \theta^{(t)})$时，$ELBO=\log p(x|\theta)$，Expectation就是ELBO，这时

  $$\begin{array}{rl} p(x|\theta) & = ELBO\\ & = \int_z q(z)\cdot \log\frac{p(x,z|\theta)}{q(z)}dz\\ & = \int_z p(z|x,\theta^{(t)})\cdot\log\frac{p(x,z|\theta)}{p(z|x,\theta^{(t)})}dz \end{array}$$

  $q(z)$能取到后验$p(z|x,\theta)$是最佳的q，实际情况后验是intractable的话，q无法取到后验$p(z|x,\theta)$.

• M-step固定q调整$\theta$：期望ELBO是关于$\theta$的函数，选择$\theta$使期望最大

  $$\begin{array}{rl} \theta^{(t+1)} & = \arg\max\limits_{\theta}p(x|\theta) = \arg\max\limits_{\theta}ELBO\\ & = \arg\max\limits_{\theta}\int_z p(z|x,\theta^{(t)})[\log p(x,z|\theta) - \log p(z|x,\theta^{(t)})]dz\\ & = \arg\max\limits_{\theta}\int_z p(z|x,\theta^{(t)})\log p(x,z|\theta)dz \end{array}$$

即为EM算法的迭代公式$(1)$。

EM算法的E、M步，都是在增大ELBO。M步使用的q是由E步$\theta^{(t)}$得到的（$q(z)=p(z|x,\theta^{(t)})$），q不等于$\theta^{(t+1)}$对应的后验分布$p(z|x,\theta^{(t+1)})$。所以一轮E、M迭代之后，会产生大于0的KL divergence，所以log-likelihood $\log p(x|\theta)$的增加量，大于ELBO的增加量，所以下一轮还有继续提高的空间（跟收敛性的证明有联系）。

另外，EM公式的推导也可以通过Jenson不等式得到，详见参考资料[1]第3集：

$$\begin{array}{rl} \log p(x|\theta) & = \log\int_z p(x,z|\theta)dz\\ & = \log\int_z\frac{p(x,z|\theta)}{q(z)}q(z)dz\\ & = \log E_{q(z)}[\frac{p(x,z|\theta)}{q(z)}]\\ & \ge E_{q(z)}[\log\frac{p(x,z|\theta)}{q(z)}]\\ & = ELBO \\ \end{array}$$

$\frac{p(x,z|\theta)}{q(z)}$为常数时等号成立，可证明$q(z)=p(z|x,\theta)$.

2.2. Q函数与ELBO

在证明EM算法收敛性的时候，有提到过Q函数$Q(\theta,\theta^{(t)})=\int_z p(z|x,\theta^{(t)})\cdot \log p(x,z|\theta)dz$. 很多EM算法的E-step是计算Q函数，M-step是极大化Q函数。实际上，Q函数与ELBO是一致的：

$$\begin{array}{rl} ELBO & = \int_zq(z)\cdot\log\frac{p(x,z|\theta)}{q(z)}dz\\ & = \int_zp(z|x,\theta^{(t)})\cdot\log\frac{p(x,z|\theta)}{p(z|x,\theta^{(t)})}dz\\ & = \int_zp(z|x,\theta^{(t)})\cdot\log p(x,z|\theta)dz - \int_zp(z|x,\theta^{(t)})\cdot\log p(z|x,\theta^{(t)})\\ & = Q(\theta, \theta^{(t)}) + const \end{array}$$

本文一开始的EM算法的公式$(1)$，用的就是Q函数的形式。

3. 广义EM

EM算法必须要求后验$p(z|x,\theta)$是tractable的，这样才可能$q(z)=p(z|x,\theta)$；如果$p(z|x,\theta)$是intractable的，则找不到$q(z)=p(z|x,\theta)$了。当p是intractable时，无法使用EM算法，只能用其他如变分推断或者MCMC采样的方法近似求出后验。

广义的EM：

如果后验p是intractable的，（ELBO=$L(q, \theta)$）

• E-step就不再是$q(z)=p(z|x, \theta^{(t)})$了，而是（固定$\theta$）$q^{(t+1)} = \arg\min\limits_{q} KL(q||p)=\arg\max L(q,\theta^{(t)})$
• M-step就是（固定$q^{(t+1)}$）$\theta^{(t+1)}=\arg\max\limits_{\theta}L(q^{(t+1)}, \theta)$

ELBO的分解：

ELBO = $E_{q(z)}[\log p(x,z|\theta) - \log q(z)]=E_q[\log p(x,z|\theta)]+ H(q)$

图解：

最后，引用一张PRML里的图（书中Figure 9.14）解释EM算法的迭代过程

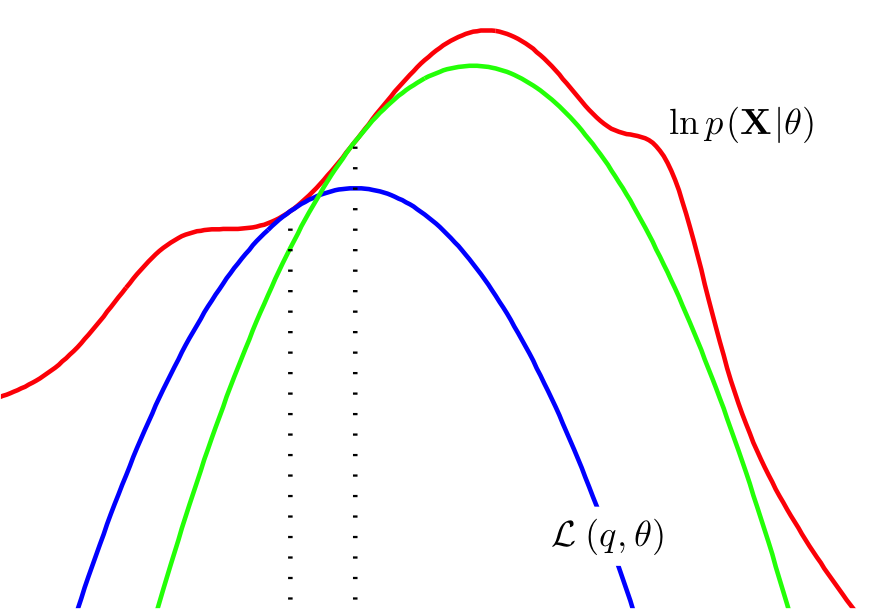
这里的$L(q,\theta)$就是ELBO，所以EM算法的实质就是每次迭代尽可能的让ELBO增大，$\log p(X|\theta)$增大。不过，EM算法不能保证找到全局最优解。

4. References

1. 机器学习-白板推导系列(十)-EM算法（Expectation Maximization）
2. PRML Chapter 9.4
3. EM算法存在的意义是什么？ - 史博的回答 - 知乎：我们这篇文章只介绍到了第1、2、4层境界