VAE是一个生成模型,生成模型一般具有两个基本功能:密度估计$P(X)$和生成样本[2]。本文先从一些其他的模型,比如GMM和Auto-Encoder,来引入VAE,这样可以更好的理解什么是VAE。然后再解释VAE的理论细节。
1. 从GMM到VAE
VAE也是latent variable model. 如果GMM是K个高斯分布的混合,那么VAE是无限多个高斯分布的混合。高斯分布只有K个高斯分布的混合$P(Z)=p_k$,无法处理复杂的任务,只能做简单的聚类。
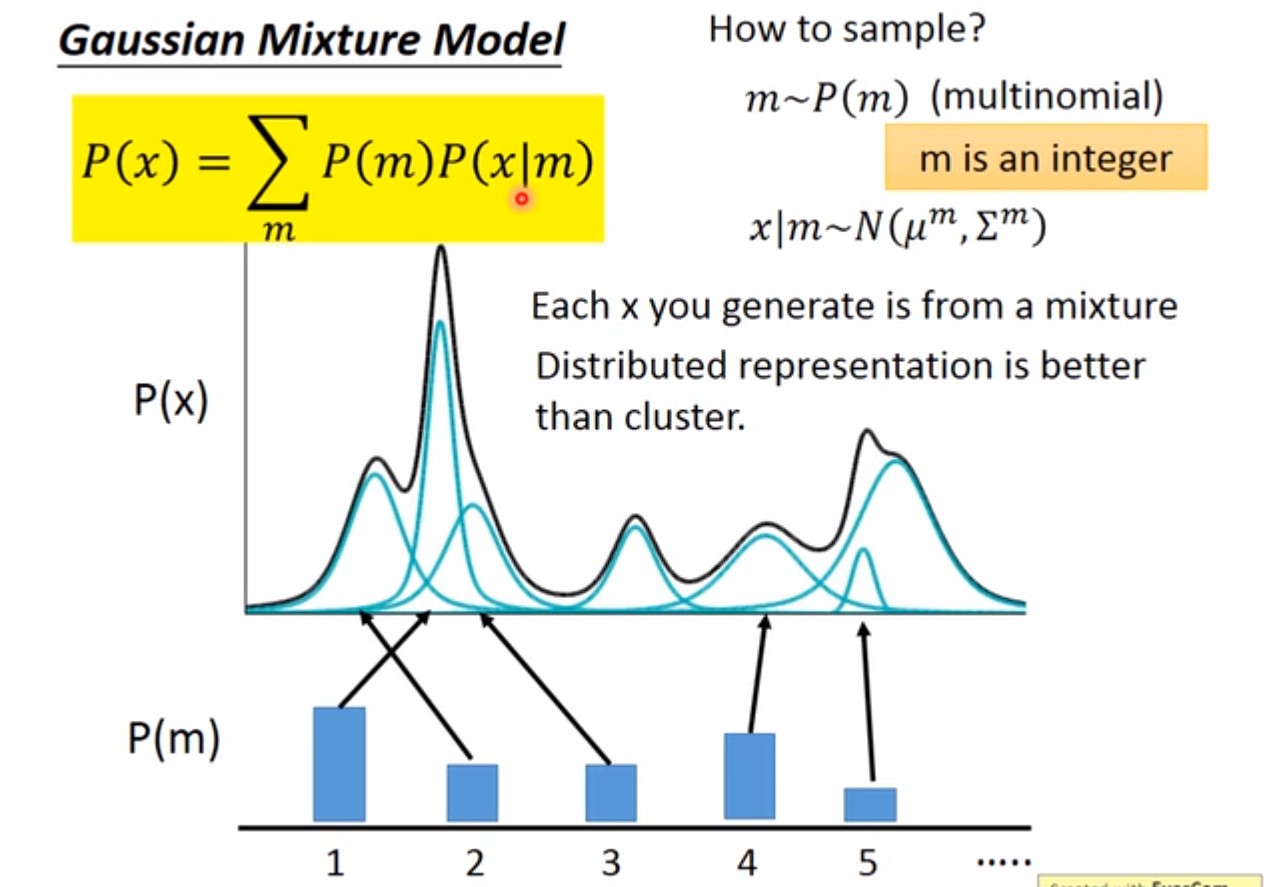
但实际中样本绝不仅仅属于某几个类那么简单,用distributed representation比聚类会更好的表示样本:样本有不同的latent attributes,比如关于疾病的人口样本的latent attributes有职业、生活习惯等等,所以latent attributes可以用向量来描述各个不同的attribute(多维的),而且服从某种分布[3]。VAE就是GMM的distributed representation版本,是GMM的推广。
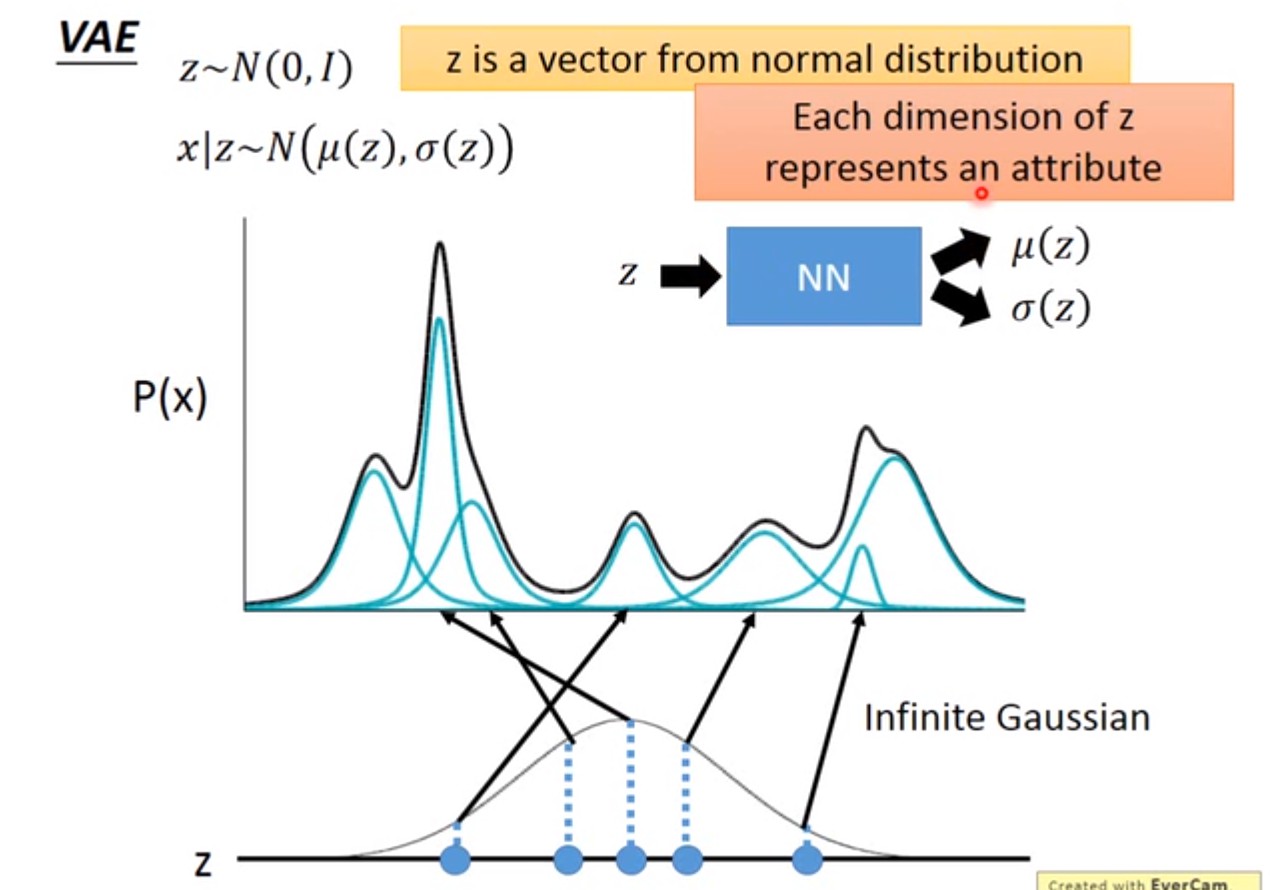
一般假设VAE的latent attritbutes服从高斯分布$Z\sim N(0,I)$,是连续的+高维的。从这个分布Z中采样得到一个向量z,向量z的每一个维度,代表一种latent attribute. 上图假设Z是一维的高斯分布,实际上可以是高维的高斯分布。采样得到z之后,可以根据z来决定X的分布。相比GMM,只有K个不同的$\mu,\Sigma$,但在VAE中,z的采样有无穷多种可能,所以$\mu,\Sigma$也有无穷多种可能。如何做到$\mu,\Sigma$也有无穷多种可能呢?把$\mu,\Sigma$看成是关于z的函数(神经网络就是一个函数)!如果X是连续的,$X|z\sim N(\mu(z), \Sigma(z))$.
因为Z是高维的,所以上面的积分,即$p(X)$是intractable,所以后验是intractable.
2. 从Auto-Encoder到VAE
VAE指的是Variational Auto-Encoder,这一节就讨论Auto-Encoder与VAE之间的关系。
Auto-Encoder是由encoder和decoder两部分组成,样本经过encoder变成一段code,code再通过decoder变回去,希望输出的结果与样本越接近越好(code往往是比样本有更低的维度)。训练完Auto-Encoder之后,可以把decoder单独拎出来,给decoder输入任意的code,就会得到不同的样本,起到了生成模型的作用。
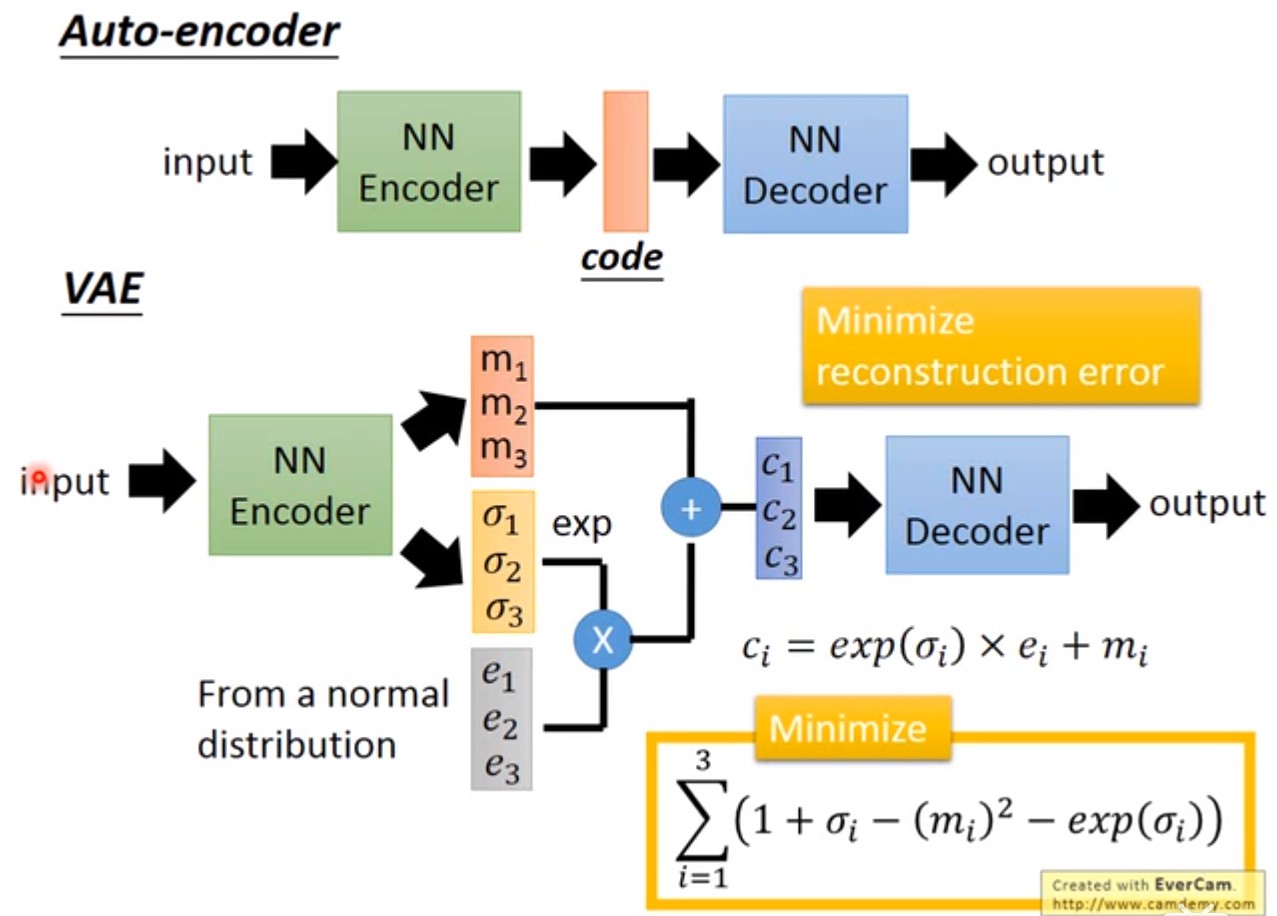
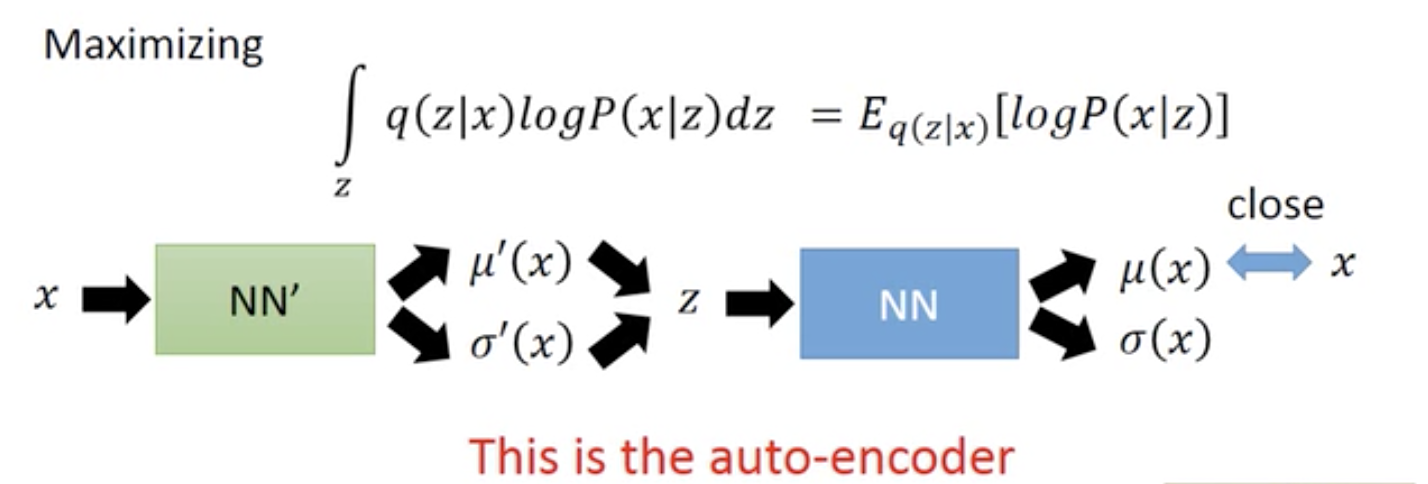
VAE同样有encoder和decoder,与Auto-Encoder不同的是:中间得到的不是确定性的code,而是一个分布(或分布的参数)。上图中的latent attributes是三维的,所以先输出1组三维的均值向量和1组三维的方差向量,然后用标准高斯分布采样得到另外一组三维的向量,最后得到的向量$c$才对应着Auto-Encoder里面的code. 上图中的两个极小化的目标函数后面再解释。
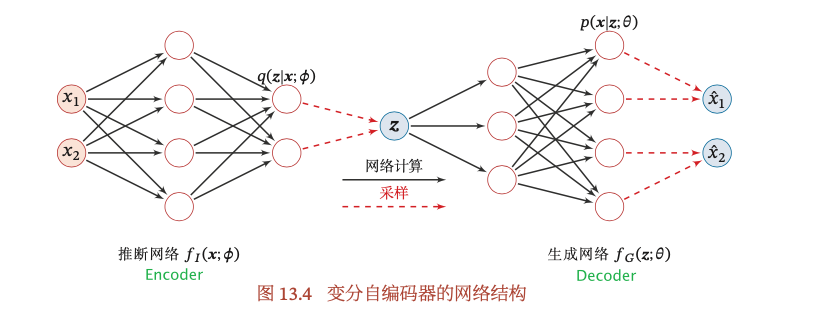
注意:VAE中间步骤得到分布的参数,与神经网络里面的参与不是一回事。分布的参数是根据样本得到的确定值,是encoder的输出$\mu’(x), \Sigma’(x)$. 与上一节相类似(尽管GMM小节实际上解释的是decoder),得到的$\mu’,\Sigma’$是关于输入x的函数。输入x不同,$\mu’(x), \Sigma’(x)$也不同。
2.1. VAE比Auto-Encoder的优势
可以参照李宏毅课件的满月和弦月的例子[3]:
Auto-Encoder无法保证样本之外的code,会得到怎样的结果:假设有一张满月的图片,对应一个code,一张弦月的图片,对应另外一个code。我们想要得到一张介于满月和弦月之间的照片,理论上只需要取两个code的中间的一组向量即可,但神经网络内部是非线性的,无法保证得到的结果。只能保证已知的样本,能够尽可能高的还原。
VAE给满月(弦月)encode的时候,会额外给code引入noise(参数$\Sigma$),在noise范围内的code,经过decoder回去之后都应该还是满月(弦月)。正因为引入了noise,所以满月和弦月对应的code可能会重合一部分(就是中间的那一段)。假设目标函数的极小化MSE,那么这个部分的code,将既跟满月有点像,又跟弦月有点像,就是一张介于满月和弦月之间的图。
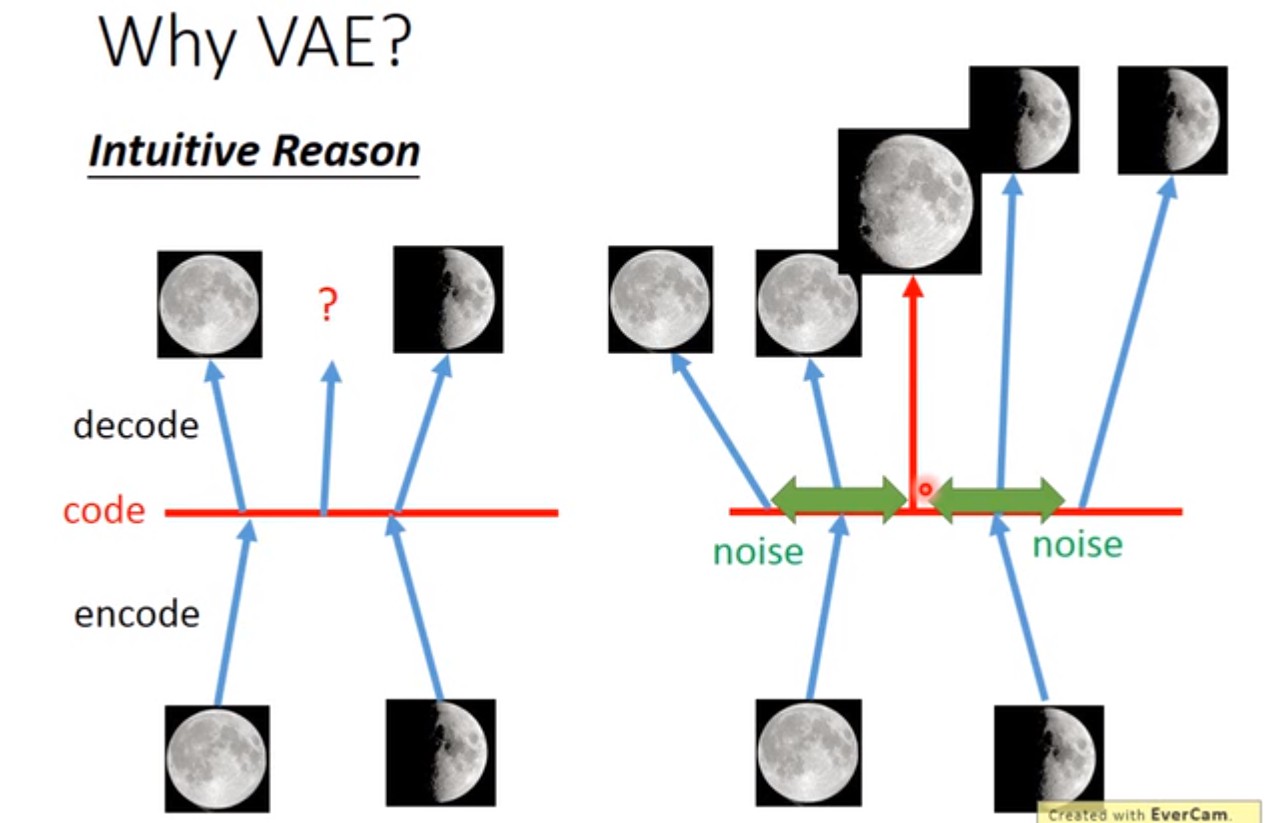
可以认为,经过encoder之后得到的$\mu(x)$就是Auto-Encoder的code;得到的$\Sigma(x)$是noise的variance. Decoder要根据加入noise之后的code,再重新构造得到原来的输入。但如果不加任何措施,算法会自动学习到noise的variance是0,构建误差是最小的,这就变回Auto-Encoder了。所以需要加一下限制,强迫variance不能太小,目标函数就多了一个正则项,后面再展开。
3. VAE中的变分
VAE是变分的Auto-Encoder,如何理解变分呢?变分推断是寻找 一个简单分布$q(z)$来近似条件概率密度$p(z|x)$,条件概率$p(z|x)=p(x,z)/p(x)=p(x,z)/\int p(x,z)dz$,在第一小节“从GMM到VAE”的最后也提到了,计算积分不可行,所以找一个简单的分布尽可能的接近$p(z|x)$,这在EM算法以及变分推断的文章中均有提到。
回顾生成模型的一个基本功能就是密度估计,所以还是极大似然$\log p(X)$.
VAE是调节神经网络里面的参数,得到encoder的函数$\mu’(x),\Sigma’(x)$,从分布$q(z|x)= N(\mu’(x),\Sigma’(x))$中采样得到z;decoder的函数$\mu(z),\Sigma(z)$,再从分布$N(\mu(z),\Sigma(z))$中采样得到输出$\hat{x}$,最终目的是使得log-likelihood达到最大。
变分$q(z)$的分布与原始的后验概率$p(z|x)$的参数是不同的(两个不同的神经网络的参数),所以记为$q_{\phi}(z)$和$p_{\theta}(z|x)$更加容易区分,而且VAE的encoder得到的分布的参数(即$\mu,\Sigma$)是关于x的函数,所以$x$是固定的值,$q$可以是任意分布,因此记为$q_{\phi}(z|x)$. 用EM算法的公式来求$q_{\theta}(Z|X)$:
$p(z)$是已知的高斯分布(第一小节的假设),剩下的事情就是找$q_{\phi}(z|x)$和$p_{\theta}(x|z)$,使得ELBO达到最大。这里引入的$q_{\phi}(z|x)$,与$\log p(x)$没有关系,所以通过调节变分q不会改变$\log p(x)$的大小,只是保证ELBO在增大,KL divergence在减小。又因为$\log p(x)$一定不小于ELBO,持续这样下去,一定会使$\log p(x)$达到最大。另外,如果最大化了ELBO,同时也会最小化$KL(q_{\phi}(z|x), p_{\theta}(z|x))$,得到的$q_{\phi}(z|x)$是$p_{\theta}(z|x)$的近似。
4. VAE的目标函数
我们现在已经知道了通过变分法,要同时找到$q_{\phi}(z|x)$和$p_{\theta}(x|z)$,使得ELBO达到最大。下面就是研究$q_{\phi}(z|x)$和$p_{\theta}(x|z)$与VAE目标函数与之间的关系,以及$q_{\phi}(z|x)$、$p_{\theta}(x|z)$与encoder、decoder之间的关系。
上一节已经解释了,让ELBO越来越大,等同于log-likelihood越来越大,所以总的目标函数就是最大化ELBO:
4.1. $\min KL(q_{\phi}(z|x), p(z))$
$q_{\phi}(z|x)$本质上是什么?给定一个x,得到一个因变量z,其实$q_{\phi}(z|x)$就是Encoder。这一项是要求$q_{\phi}(z|x)$尽可能的与$p(z)$接近,也就是调节encoder,使得x对应的分布$N(\mu’(x),\Sigma’(x))$与$p(z)=N(0,I)$越接近越好。
参考paper[5],$\min KL(q_{\phi}(z|x), p(z))$就是目标函数中的正则项,呼应了前面提到的加入正则项的事情,目的是使得noise的variance不是0,否则就变回Auto-Encoder啦。
4.2. $\max\int_zq_{\phi}(z|x)\log p_{\theta}(x|z)dz$
$\int_zq_{\phi}(z|x)\log p_{\theta}(x|z)dz = E_{q_{\phi}(z|x)}[\log p_{\theta}(x|z)]$,指的是按照$q_{\phi}(z|x)$的权重来对$\log p_{\theta}(x|z)$求期望。本质上这一项就是Auto-Encoder的功能:给定x,经过encoder,即$q_{\phi}(z|x)$,得到$\mu’(x)$和$\Sigma’(x)$,根据这两个参数对应的分布,采样得到z;得到z之后再最大化产生回x的概率,也就是z经过decoder,即$p_{\theta}(x|z)$,得到$\mu(z)$和$\Sigma(z)$,然后根据这两个参数对应的分布采样得到x。因此这一项就是Reconstruction Loss,让输入的x与输出的x尽可能的接近。
[2]通常情况下,这一项可通过采样的方式近似计算。对于每个样本$x$,根据$q_{\phi}(z|x)$采样M个$z^{(m)}, ~1\le m\le M.$
本来这一项与参数$\phi$有关,经过上面的采样,这一项变得与参数$\phi$无关。当神经网络使用梯度下降法来学习参数时,采样之后的近似值关于$\phi$的梯度为0,这是因为$z$与$\phi$之间不再是确定性关系,而是采样关系,需使用重参数化技巧来解决,后面再解释。
4.3. VAE中的Encoder和Decoder
- Encoder的目标是是使得$q_{\phi}(z|x)$ 尽可能接近真实的后验$p_{\theta}(z|x)$, 需要找到一组网络参数来最小化两个分布的KL散度,即. 这一般无法直接计算,VAE是通过最大化ELBO间接使得KL散度最小化,因此VAE的Encoder目标是找到一组网络参数$\phi^*$使得ELBO最大化。
- Decoder的目标是找到一组网络参数$\theta^*$使得ELBO最大化。
综上,$q_{\phi}(z|x)$是decoder对应的神经网络;$p_{\theta}(x|z)$是encoder对应的神经网络。从EM算法的角度看,Encoder和Decoder分别可以看成是EM算法的E步和M步。目标函数分为两部分,一个是Reconstruction Loss(Decoder),另一项是正则化项(Encoder)。
5. 重参数化技巧
一般假设$Z|X\sim N(\mu_{\phi}(X), \Sigma_{\phi}(X))$,$z$是经过采样得到的,所以$z$和$\phi$之间不是确定性关系,无法直接对$z$关于$\phi$求导数。可通过重参数化技巧,将$z$和$\phi$之间的随机性采样关系变成确定性关系。引入一个随机变量$\epsilon\sim N(0,I)$,假设$q_{\phi}(z|x)$服从正态分布$N(\mu_{\phi},\Sigma_{\phi})$,其中$\mu_{\phi},\Sigma_{\phi}$是Encoder的输出,依赖于参数$\phi$,通过
再参数化,这样$z$和$\phi$之间的关系变成确定性的,使得$Z|X\sim N(\mu_{\phi}(X), \Sigma_{\phi}(X))$的随机性独立于$\phi$,可以求$z$关于$\phi$的导数。
6. VAE的learning、inference问题
知道了VAE的encoder、decoder以及目标函数,后面就是如何去训练这个模型,也就是确定神经网络的参数,进而确定分布的参数$<\theta,\phi>$用于采样,在概率生成模型中也称为learning问题。训练结束之后,参数已经确定,使用先验概率$p(z)$采样用于生成样本,也称为inference问题。
训练时如果用EM算法的公式
- E-step: 当$q=p_{\theta}(Z|X)$时,KL divergence=0,Expectation is ELBO
- M-step: $\theta = \arg\max\limits_{\theta} ELBO = \arg\max\limits_{\theta} E_{p_{\theta’}(Z|X)}[\log p_{\theta}(X, Z)]$
VAE无法使用EM算法来解决,因为EM算法的前提是后验概率$p_{\theta}(Z|X)$为tractable的。但因为$p_{\theta}(Z|X)$是intractable,我们需找到$q_{\phi}(Z|X)$来逼近它:
上式对$\theta$或$\phi$求梯度,就可以得到想要的参数值,具体的过程可参考变分推断的求解。VAE是用神经网络训练来确定参数,而不是使用传统的变分推断方法。在learning过程中,先从X到Z,然后再从Z到X,就是从encoder到decoder的过程。训练过程的encoder和decoder的参数是同时学习的。
经过重参数化,VAE可通过梯度下降来学习神经网络里面的参数$\phi,\theta$。
对每个样本$x^{(i)}$,对随机变量$\epsilon$做M次采样$\epsilon^{(i,m)},~1\le m\le M$,并用重参数化技巧的公式$z^{(i,m)} = \mu_{\phi}(x) + \Sigma_{\phi}^{1/2}(x)\cdot\epsilon^{(i,m)}$计算得到$z^{(i,m)}$. 这样VAE的目标函数可写为:
如果是随机梯度下降,每次只采集一个样本和一个随机变量$\epsilon$,并假设$p_{\theta}(x|z)$服从高斯分布$N(\mu_{\theta},\lambda I)$,其中$\mu_{\theta}$为encoder的输出,$\lambda$为超参数,则VAE的目标函数可简化为:
原本的梯度下降是对每一个样本x经过encoder之后的隐变量z进行多次采样的,随机梯度下降只采样一次。
第一项是简化之后的Reconstruction Loss,即x与decoder分布的均值之间的距离;第二项是化简之后的正则化项,超参数$\lambda$可认为是正则化系数。这与Auto-Encoder的目标函数非常类似,但本质上是不同的。
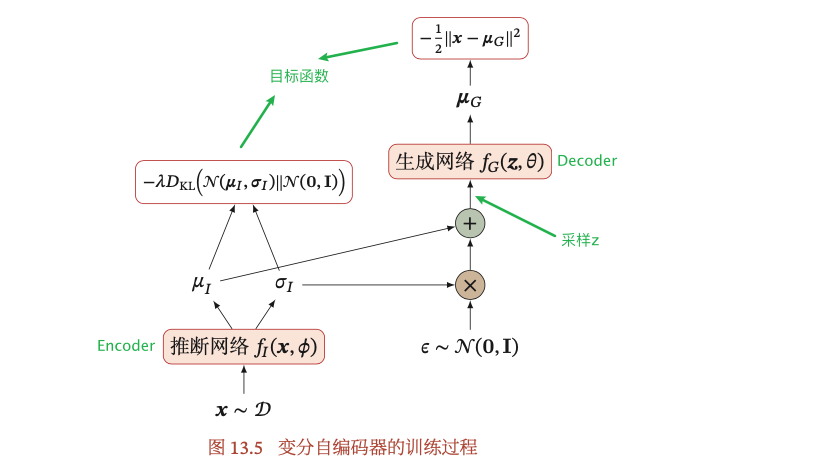
训练过程中,decoder对应的$p_{\theta}(x|z)$里面的z,不是先验概率$p(z)$里面的z,decoder的z是由encoder $p_{\theta}(z|x)$得到的分布采样而得到的z。训练结束后,inference可用先验概率$p(z)$进行采样,用于生成样本。