拉普拉斯矩阵与拉普拉斯算子

[1] GCN提取特征的方式不是spatial的，而是spectral的，基于spectral graph theory来实现图上的卷积操作。Spectral graph theory是借助图的拉普拉斯矩阵的特征值和特征向量来研究图的性质。本文就是介绍什么是拉普拉斯矩阵、拉普拉斯算子，以及它们之间的关系。

1. 拉普拉斯矩阵

给定图$G=(V,E)$，

• 定义$D$是顶点的度矩阵（对角阵），对角线上的元素依次为各个顶点的度数
• 定义$A$是邻接矩阵，如果$v_i$与$v_j$有边相连，那么$A_{ij}=1$；反之$A_{ij}$为0. 显然无向图的邻接矩阵为对称矩阵。

• 定义拉普拉斯矩阵$L=D-A$，如下图所示
  

• 拉普拉斯矩阵的其他形式（归一化形式）：$L^{sys}=D^{-1/2}LD^{-1/2}$，$L^{rw}=D^{-1}L$

1.1. 拉普拉斯矩阵的性质

1. L是对称矩阵，可以进行特征分解（谱分解）
2. L是半正定矩阵，所以L的每个特征值非负

1.2. 拉普拉斯矩阵的特征分解（谱分解）

首先明确一点，不是所有的矩阵都可以特征分解，其充要条件是n阶方阵存在n个线性无关的特征向量。

拉普拉斯矩阵是半正定的对称矩阵，有下面三个性质：

1. 实对称矩阵一定有n个线性无关的特征向量
2. 半正定矩阵的特征值一定非负
3. 实对称矩阵的特征向量总可以化成两两正交的正交矩阵

由性质1可知，拉普拉斯矩阵一定可以特征分解。假设拉普拉斯矩阵的特征分解为：

$$L=U \begin{pmatrix} \lambda_1&&\\ &\dots&\\ && \lambda_n \end{pmatrix} U^{-1}$$

由性质2可知，$\lambda_i\ge 0~(1\le i\le n)$. 由性质3可知，$U=(u_1,u_2,\dots,u_n)$是列向量为单位特征向量的矩阵，且U是正交矩阵，即$UU^T=I$，所以L的特征分解也可以写成：

$$L=U \begin{pmatrix} \lambda_1&&\\ &\dots&\\ && \lambda_n \end{pmatrix} U^{T}$$

总结：

2. 拉普拉斯算子

2.1. 函数的拉普拉斯算子

令$\Delta$是拉普拉斯算子，$f$是欧氏空间中的二阶可微实函数，$\Delta f$就是欧氏空间中求$f$的二阶微分之和（散度）。例如函数$f(x,y,z)$有三个变量，$\Delta f=\frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2}+\frac{\partial^2 f}{\partial z^2}$，散度是一个标量。

以上是拉普拉斯算子传统的定义，但这个定义不容易推广到图上，因为图上没有二阶可微实函数$f$，而是一组高维feature向量$f$. 所以可认为变量是离散的，$\frac{\partial^2 f}{\partial x^2}=f’’(x)\approx f’(x)-f’(x-1)=f(x+1)+f(x-1)-2f(x)$. 将拉普拉斯算子推广到二维的离散形式：

$$\begin{array}{rl} \Delta f(x,y) =& \frac{\partial^2 f}{\partial x^2}+ \frac{\partial^2 f}{\partial y^2}\\ =& f(x+1,y)+f(x-1,y)-2f(x,y) + f(x,y+1)+f(x,y-1)-2f(x,y)\\ =& f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y) \end{array}$$

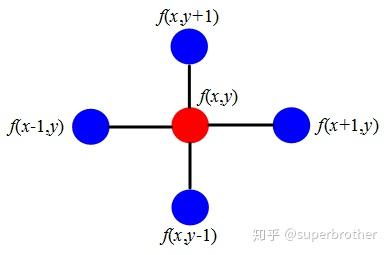
从上面的例子看出，拉普拉斯算子计算的是周围点与中心点的梯度差。

2.2. 图上的拉普拉斯算子

先说结论[3]：

拉普拉斯矩阵就是图上的拉普拉斯算子，或者说是离散的拉普拉斯算子。

假设图G有N个节点，前面的函数$f$在这里是N维向量$f=(f_1,f_2,\dots,f_N)$，其中$f_i$为节点$i$处的feature取值。

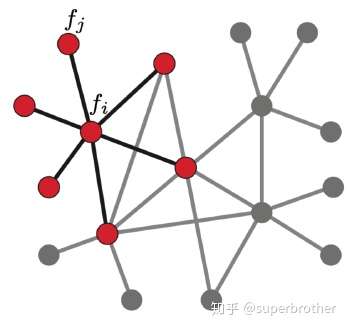
图上的拉普拉斯算子表示相邻的节点的feature值之差$\Delta f_i=\sum\limits_{j\in N_i}(f_i-f_j)$；如果边$E_{ij}$有权重$w_{ij}$，其中$w_{ij}=0$表示两点之间不相邻，则上式可写为：

$$\begin{array}{rl} \Delta f_i=& \sum\limits_{j\in N_i}w_{ij}(f_i-f_j)\\ =& \sum\limits_{j\in N_i}w_{ij}f_i - \sum\limits_{j\in N_i}w_{ij}f_j\\ =& d_if_i - (w_{i1},w_{i2},\dots,w_{iN})\cdot(f_1,f_2,\dots,f_N)^T\\ \Delta f=& \begin{pmatrix}\Delta f_1\\\vdots\\\Delta f_N\\\end{pmatrix}= diag(d_i)f-Wf=(D-W)f=Lf \end{array}$$

这里的$D-W$就是拉普拉斯矩阵的定义，拉普拉斯矩阵的第$i$行反应了第$i$个节点对其它所有节点产生扰动的累积增益。

3. 为什么GCN要用拉普拉斯矩阵？

在spectual graph theory里面，会将图上的信号进行傅立叶变换。而傅立叶（逆）变换的本质是找到一组正交基的线性组合来表示这个信号。正交基就可以选择拉普拉斯矩阵的特征向量。因为拉普拉斯矩阵是实对称矩阵，所以它的特征向量是n维空间中n个线性无关的正交向量，就是一组正交基。这组正交基可以用来表示图上的任意信号。

3.1. 定义一个图例

有一个4个顶点的图，图上每个点都有标量信号，组成向量$f$. 另外，可以轻易求出拉普拉斯矩阵，然后特征分解得到拉普拉斯矩阵的特征值和特征向量。那拉普拉斯矩阵的特征值与特征向量与图信号有什么关系呢？

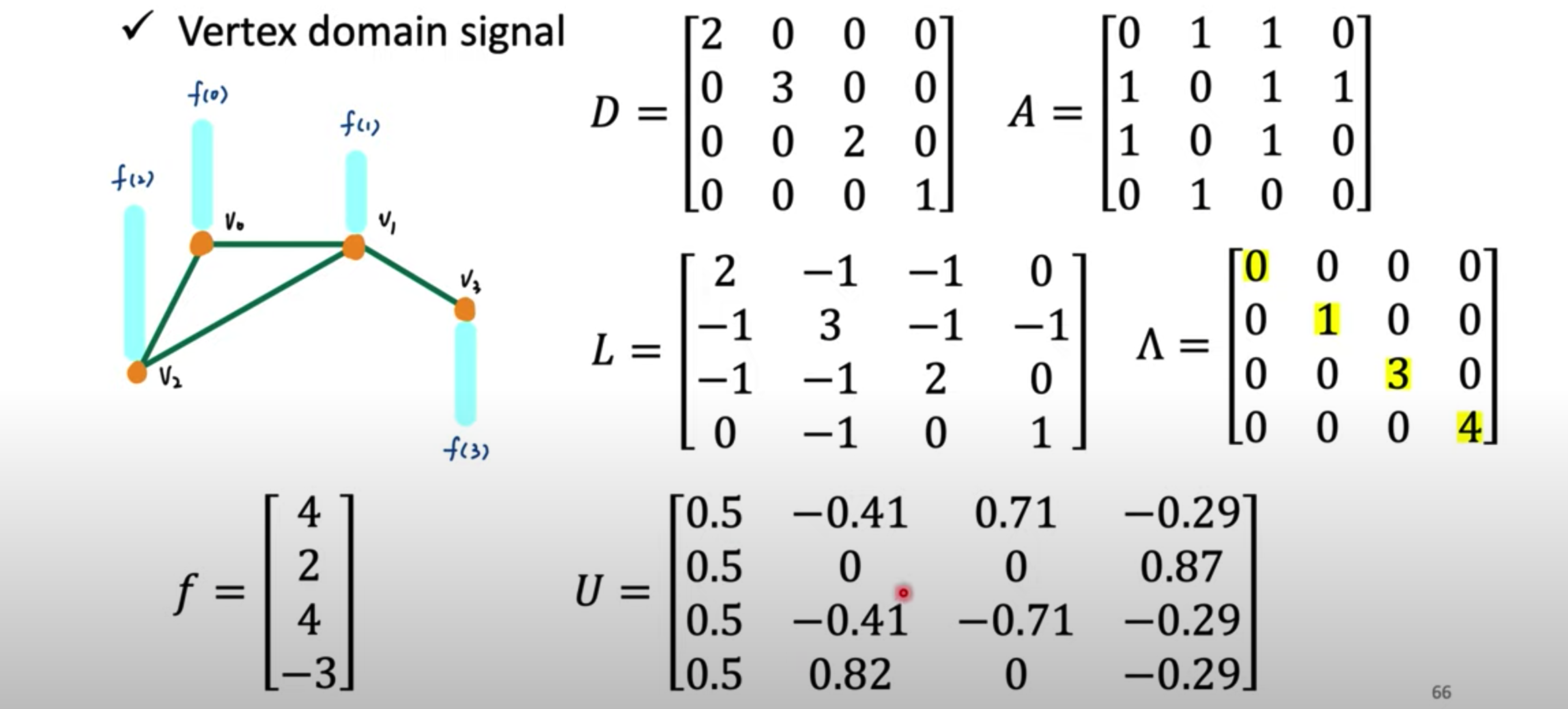
3.2. 拉普拉斯矩阵的特征向量

特征向量是4维空间下的4个正交基向量，所以这四个正交基可以线性表示这个空间下的任何向量，包括图信号$f$. 下面就是这四个向量：

3.3. 拉普拉斯矩阵的特征值

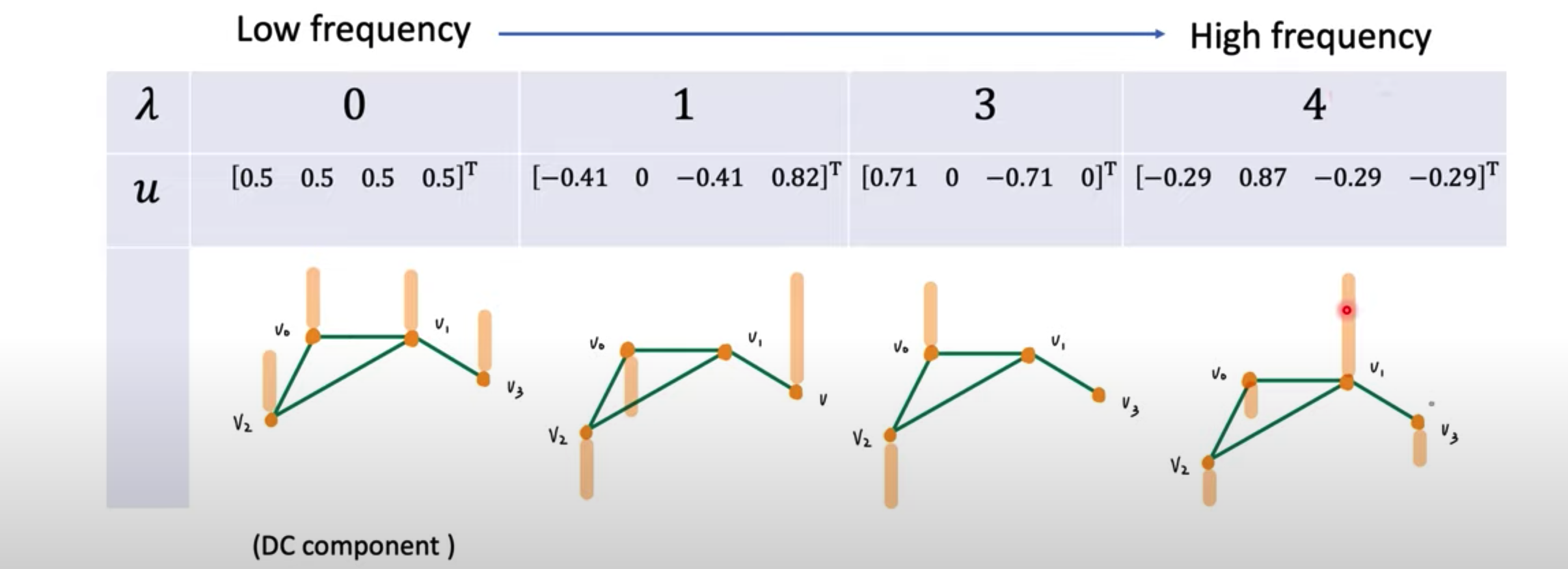
拉普拉斯矩阵的特征向量已经明白了，就是正交基；那么特征值$\lambda$在图上的意义是什么呢？在回答这个问题之前，我们先来看一下拉普拉斯矩阵$L$（即拉普拉斯算子）对图信号$f$做了什么处理：

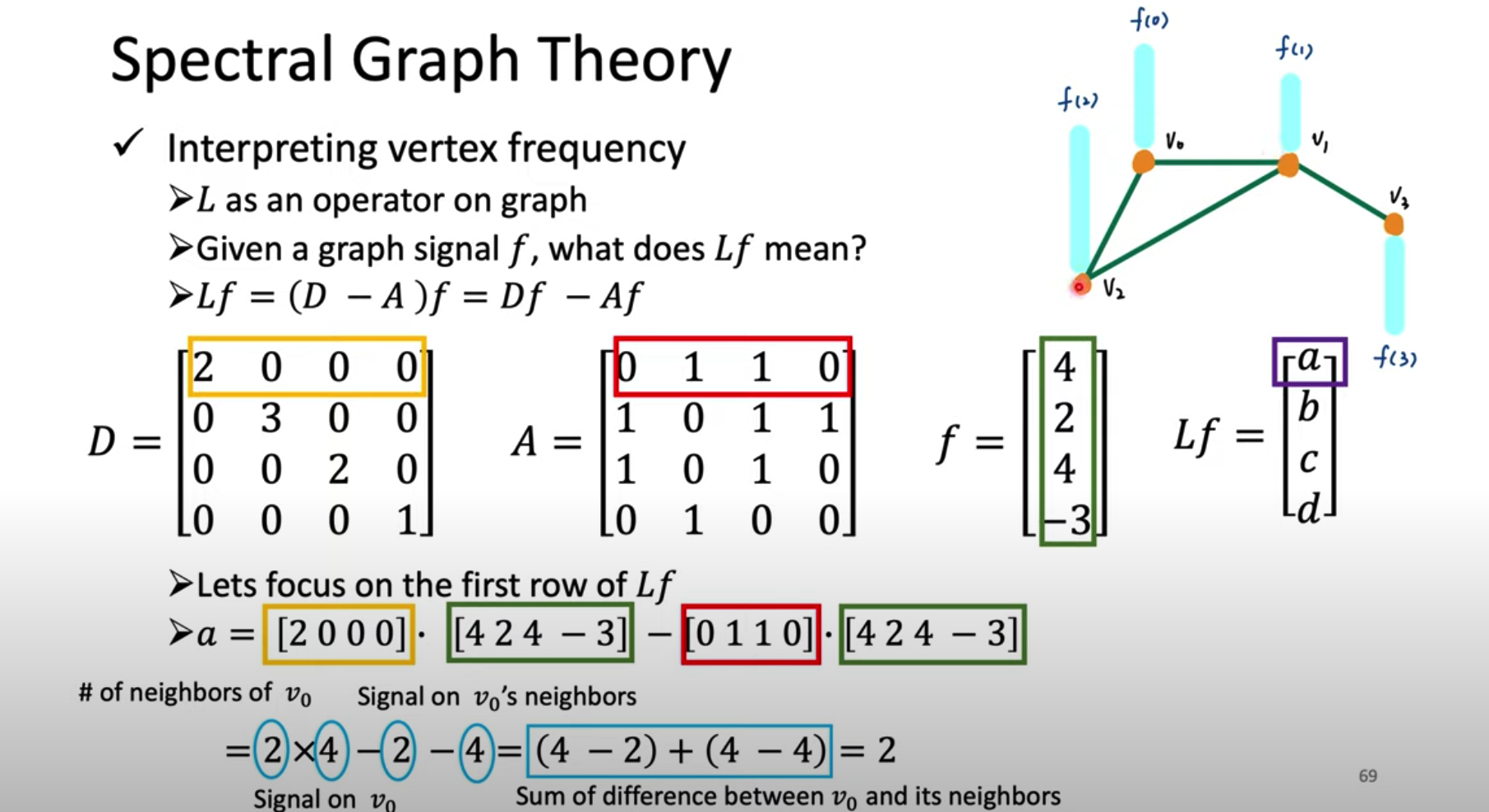
由上一节拉普拉斯算子的定义可知，$Lf$的每个元素就是这个点与所有邻居点的信号差之和。从图示可以验证，$Lf$在$v_0$节点的值为相邻的$v_1$信号之差+相邻的$v_2$信号之差。记为$(Lf)(v_i)=\sum_{v_j\in V}a_{ij}(f(v_i)-f(v_j))$，其中$a_{ij}$是邻接矩阵$A$的第$(i,j)$个元素。

单纯的差值可能有正有负，如果真想表达每个点与邻居点之间信号的差异大小，需要用平方的形式，定义如下：

$$\begin{array}{rl} f^TLf &= \sum\limits_{v_i\in V}f(v_i)\sum\limits_{v_j\in V}a_{ij}(f(v_i)-f(v_j))\\ &= \sum\limits_{v_i\in V}\sum\limits_{v_j\in V}a_{ij}(f^2(v_j)-f(v_i)f(v_j))\\ &= \frac{1}{2}\sum\limits_{v_i\in V}\sum\limits_{v_j\in V}a_{ij}(f^2(v_i)-f(v_i)f(v_j)+f^2(v_j)-f(v_j)f(v_i))\\ &= \frac{1}{2}\sum\limits_{v_i\in V}\sum\limits_{v_j\in V}a_{ij}(f(v_i)-f(v_j))^2 \end{array}$$

联想离散傅立叶变换的不同频率的基，基的频率越大，相邻两个时域信号的差异越大；基的频率越小，相邻两个时域信号越smooth。类比于图信号，如果频率越大，说明每个点与其邻居点的信号差异越大；频率越小，点与邻居点的信号差异越小。$f^TLf$就表示顶点之间的信号差异，也蕴含着频率的“概念”。

为什么特征向量对应的特征值是特征向量的频率呢？把特征向量$u_i$（图信号空间中的一个instance）代入$f^TLf$，

$$u_i^TLu_i=u_i^T\lambda_iu_i=\lambda_iu_i^Tu_i=\lambda_i$$

所以对于特征向量，点与邻居点之间的信号差异（频率）就等于特征值$\lambda_i$.

回到例子，最明显的就是$\lambda=0$时，由上面的结论，$u$中点与点之间的信号差异为0，实际上确实如此。$\lambda$越大，频率越来越高，这个特征向量的相邻点的信号差异越大。

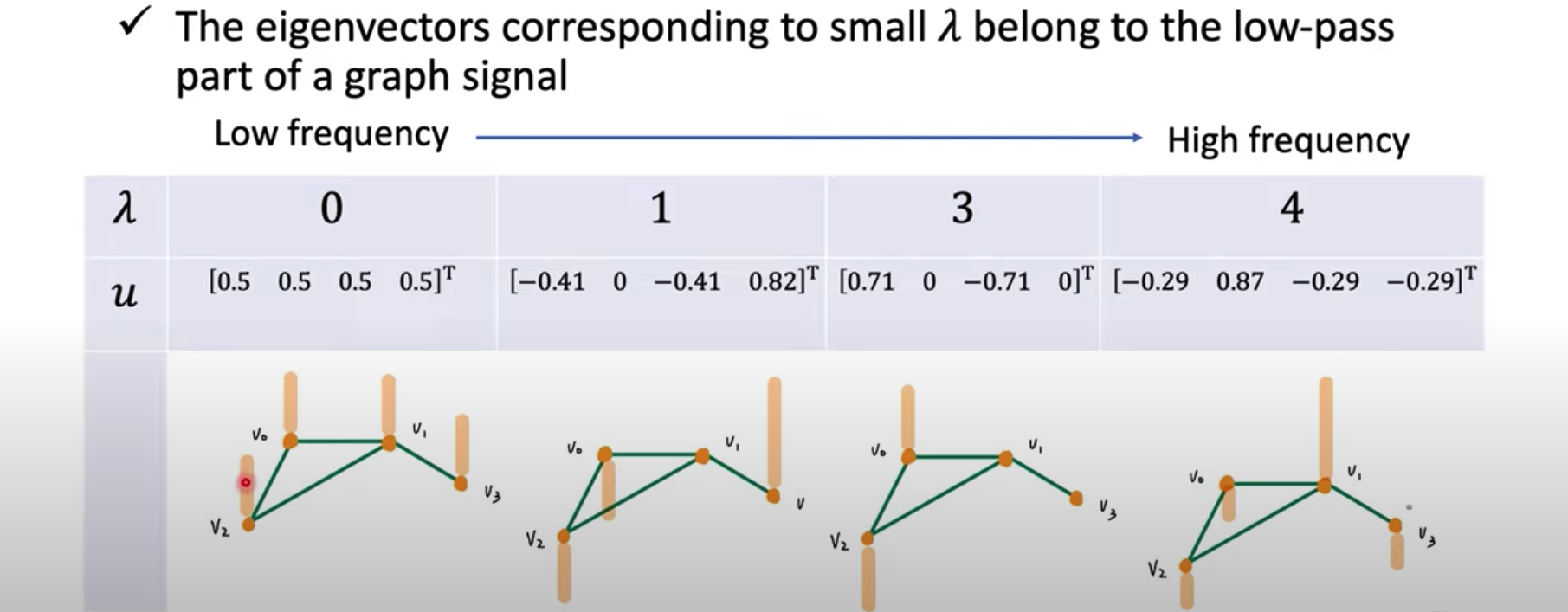
3.4. 结论

拉普拉斯矩阵以及它的特征向量和特征值，是Spectral graph theory的理论基础。通过拉普拉斯矩阵的特征向量，可以完成信号从vertex domain到spectral domain的变换，也就是图傅立叶变换。

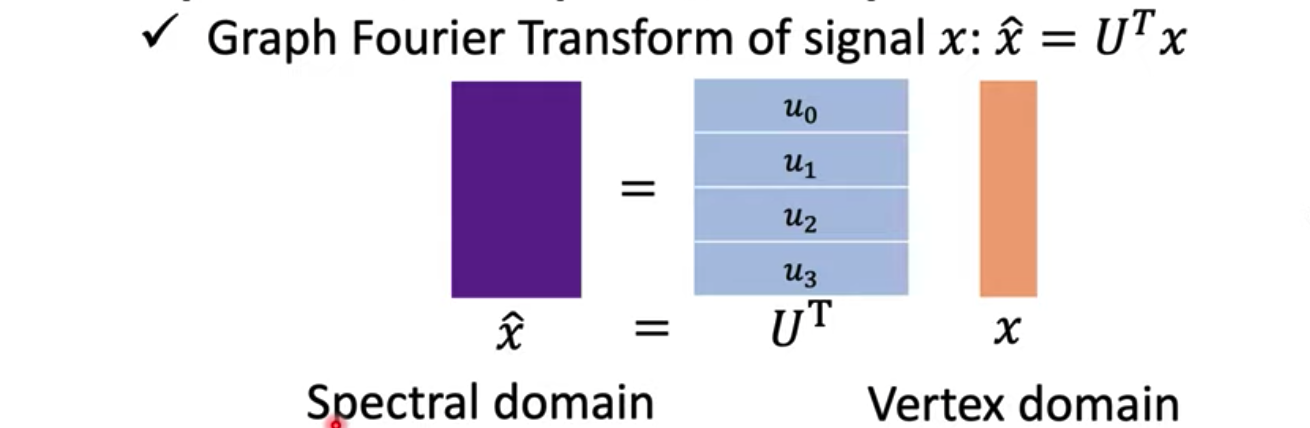
图信号（vertex domain）使用图傅立叶变换（spectral domain），加上卷积核，得到的结果再图傅立叶逆变换回去，变成新的vertex domain的图信号（graph embedding），就是GCN的大致思想了。

4. 参考资料

1. 如何理解 Graph Convolutional Network（GCN）？
2. Laplacian matrix
3. 拉普拉斯矩阵与拉普拉斯算子的关系
4. 李宏毅助教课（Graph Neural Network）Youtube