GCN

前面两篇文章分别介绍了《傅立叶变换》和《图的拉普拉斯矩阵与拉普拉斯算子》，有这两篇文章作为基础，我们终于可以学习GCN了。

GCN的理论基础是Spectral Graph Theory，Spectral Graph Theory是将图的拉普拉斯矩阵进行谱分解，用它的特征值和特征向量来表示图上的信息。这样图上的信息就由vertex domain变换到了spectral domain上，spectral domain与顶点信息没有关系了，特征向量经过卷积核运算，再图傅立叶逆变换回到vertex domain，完成graph embedding。那么拉普拉斯的特征值和特征向量与傅立叶变换有什么关系呢？本文首先讨论的图傅立叶变换，就会将前面两篇文章的知识点结合起来。

下图直观解释了GCN的基本思想：

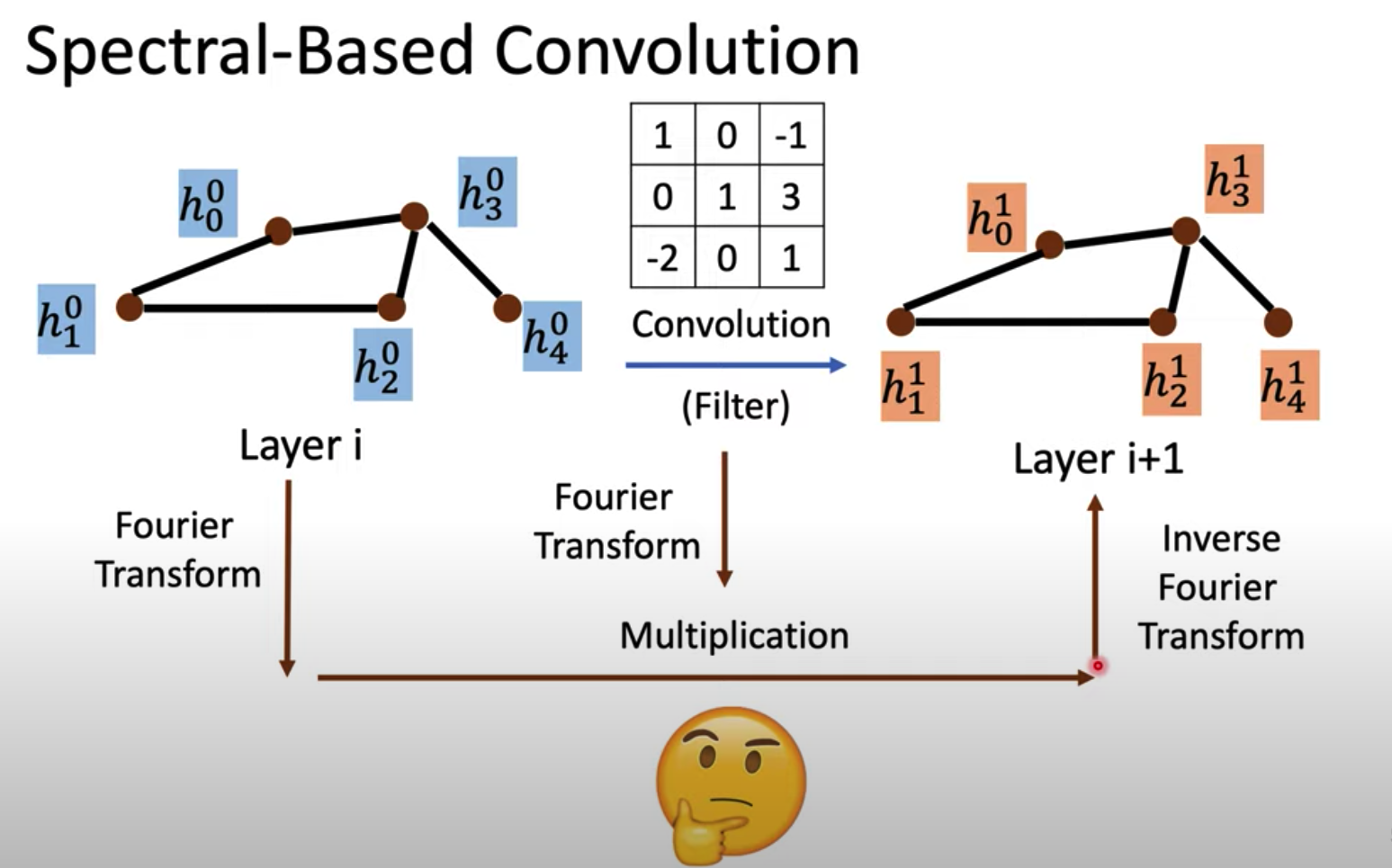
1. Graph Fourier Transform

在傅立叶变换一文中，最后的总结：

傅立叶逆变换本质是把任意一个函数表示成了若干个正交基函数的线性组合；
傅立叶正变换本质是求线性组合的系数。也就是由原函数和基函数的共轭的内积求得。

比如在传统的傅立叶变换中，就是用不同频率的三角函数作为一组正交基，它们的线性组合来表示时域信号。那图上的信号由什么来表示呢？

1.1. 图傅立叶正变换

对于图上的信号，也可以进行傅立叶变换，即找到一组正交基的线性组合来表示图的信号。那么问题就是图的信号由一组什么样的基来组成呢？

回忆传统的傅立叶变换$g(\hat{f}) =\sum\limits_{t=-\infty}^\infty F(t)e^{-2\pi i\hat{f}t}= \int_{-\infty}^\infty F(t)e^{-2\pi i \hat{f}t}dt$，令$w=2\pi\hat{f}$，那么傅立叶变换的公式为

$$g(w) = \int F(t)e^{-iwt}dt$$

即时域信号可以由一组不同频率的基函数$e^{-iwt}$的线性组合来表示。我们来观察一下这一组基$e^{-iwt}$，除了它是正交基，还满足是拉普拉斯算子的特征函数。为什么呢？

首先我们把特征向量推广到特征函数：特征向量满足$Ax=\lambda x$，把矩阵$A$推广为任意的一种变换（算子），把特征向量$x$推广为特征函数（无限维特征向量）。我们要验证基函数$e^{-iwt}$是拉普拉斯算子$\Delta=\sum\limits_{i}\frac{\partial^2}{\partial^2 x_i}$的特征函数，即

$$\Delta e^{-iwt} = \frac{\partial^2}{\partial^2 t}e^{-iwt} = -w^2e^{-iwt}$$

所以传统傅立叶变换的基$e^{-iwt}$是拉普拉斯算子的特征函数，傅立叶变换是时域信号与拉普拉斯算子特征函数的积分。由之前的《拉普拉斯矩阵与拉普拉斯算子》，图上的拉普拉斯算子就是图的拉普拉斯矩阵，所以把时域信号推广到离散的图信号上，图上的傅立叶变换是图信号与拉普拉斯矩阵特征向量的求和。

$$g(\lambda_l) = \sum\limits_{i=1}^n f(i)*u^*_l(i)$$

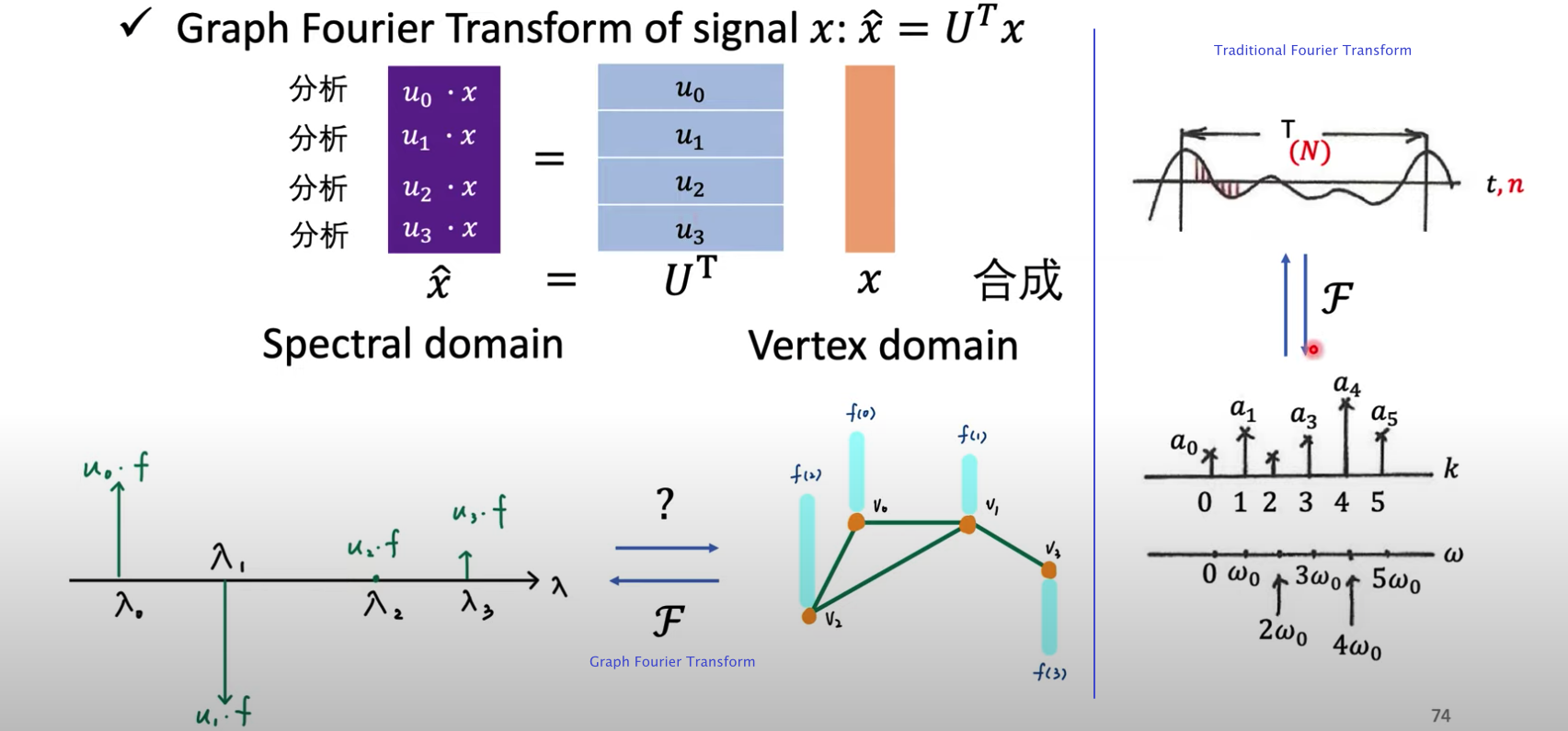
以上就是图的傅立叶变换。其中，图有n个顶点，顶点$i$上的图信号为$f(i)$（图信号对应传统傅立叶变换的时域信号）；图上拉普拉斯矩阵的n个特征向量为$u_1,u_2,\dots,u_n$，而且这n个特征向量是正交的，第$l$个特征向量的第$i$个分量是$u_l(i)$；$\lambda_l$为图拉普拉斯矩阵的第$l$个特征向量对应的特征值。上面的求和运算使用的是特征向量的共轭$u^*_l$，这是因为特征向量是定义在复平面的，为了保证正交性，所以内积用共轭，这在《傅立叶变换》一文中解释过。

将图上的傅立叶变换写成矩阵形式：

$$\begin{pmatrix}g(\lambda_1)\\g(\lambda_2)\\\dots\\g(\lambda_n)\end{pmatrix}= \begin{pmatrix}u_1(1)&u_1(2)&\dots&u_1(n)\\ u_2(1)&u_2(2)&\dots&u_2(n)\\ \vdots&\vdots&\ddots&\vdots\\ u_n(1)&u_n(2)&\dots&u_n(n) \end{pmatrix} \begin{pmatrix} f(1)\\f(2)\\\dots\\f(n) \end{pmatrix}$$

简写为$g=U^Tf$. 这里的$U$就是《拉普拉斯矩阵与拉普拉斯算子》一文中的$U$，即

$U=(u_1,u_2,\dots,u_n)$是列向量为单位特征向量的矩阵，且$U$是正交矩阵，即$UU^T=I$

下图进一步解释图傅立叶变换，假设图有4个顶点，经过傅立叶变换后的$g=U^Tf=(u_0f, u_1f, u_2f, u_3f)^T$，即图信号$f$在不同频率$\lambda$上的大小（不同频率的$\lambda$对应着不同的特征向量$u$）。

1.2. 图傅立叶逆变换

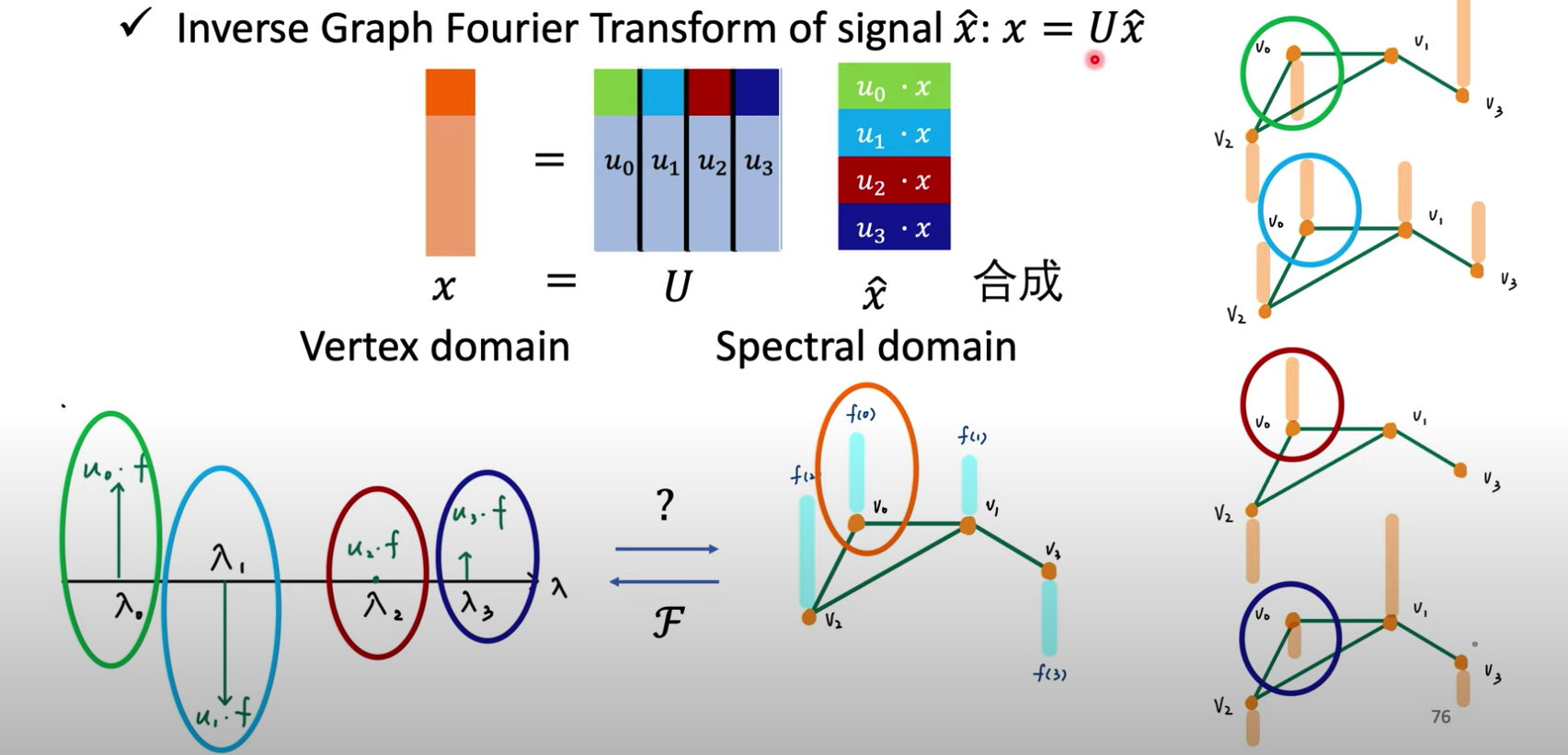
上图假设有了每个频率下图信号分量的大小（左下图），如果得到原来vertex domain的图信号呢？这就是图傅立叶逆变换。

类似的，传统傅立叶逆变换公式$F(t) = \sum\limits_{\hat{f}=-\infty}^\infty g(\hat{f})e^{2\pi i\hat{f}t}=\int_{-\infty}^\infty g(\hat{f})e^{2\pi i\hat{f}t}d\hat{f}$，令$w=2\pi\hat{f}$，则傅立叶逆变换公式为$F(t)=\frac{1}{2\pi}\int_{w}g(w)e^{iwt}dw$，从频域变换到时域。在图傅立叶逆变换中，从频域信号变换到图上的信号，

$$f(i) = \sum\limits_{l=1}^n g(\lambda_l)u_l(i)$$

将图上的傅立叶逆变换写成矩阵形式：

$$\begin{pmatrix} f(1)\\f(2)\\\dots\\f(n) \end{pmatrix}= \begin{pmatrix}u_1(1)&u_2(1)&\dots&u_n(1)\\ u_1(2)&u_2(2)&\dots&u_n(2)\\ \vdots&\vdots&\ddots&\vdots\\ u_1(n)&u_2(n)&\dots&u_n(n) \end{pmatrix} \begin{pmatrix}g(\lambda_1)\\g(\lambda_2)\\\dots\\g(\lambda_n)\end{pmatrix}$$

简写为$f=UU^{-1}f=UU^Tf=Ug$.

延续上图的例子，假设要得到顶点$v_0$的图信号$f(v_0)$，就是把正交基的第一个分量相应的乘以频率的分量，非常直观！

1.3. 两点疑问revisited

1. 为什么拉普拉斯矩阵的特征向量可以作为图傅立叶变换的基？
   傅立叶变换的本质是把一个函数表示称一组基函数的线性组合。通过前面的公式看出，图上的信号$f(i)$，其中$i$是顶点，可以表示成拉普拉斯矩阵特征向量的线性组合。因为拉普拉斯矩阵的特征向量$u_1,u_2,\dots,u_n$是n维空间（n个顶点）下n个线性无关的正交向量，所以这组特征向量构成空间的一组基，可以表示任意信号$f(i)$. 另外一个解释的角度比较难懂，姑且看之。

2. 为什么拉普拉斯矩阵的特征值表示的频率是什么？

   这个问题更好的解释请移步《拉普拉斯矩阵与拉普拉斯算子》一文最后一节。在图上确实无法直观的展示“频率”这个概念。至少经过图傅立叶变换，顶点的信号被变换成了“频率”信号，从此我们在spectual domain上研究问题，而不是在vertex domain上了。将拉普拉斯的n个特征值从小到大排列，$\lambda_1\le\lambda_2\le\dots\lambda_n$，因为拉普拉斯矩阵是半正定的，所以这些特征值都非负。而且最小的特征值$\lambda_1=0$，这是因为全1向量也是拉普拉斯矩阵的特征向量（拉普拉斯矩阵的定义），对应的特征值为0。在图的n维空间中，越小的特征值$\lambda_l$代表着特征向量$u_l$的占有的份量越少，是可以忽略的低频部分。这个跟图像压缩、PCA降维有异曲同工之妙，都是把特征值小的部分变成0，保留特征值大的部分。

2. 图卷积

2.1. 函数卷积定义

关于卷积的定义可以参考此回答，此问题下许多其他回答都蛮好。教科书上的定义函数$f_1, f_2$的卷积为$f_1*f_2(n)$，

• 连续形式：$f_1*f_2(n)=\int_{-\infty}^{\infty}f_1(\tau)f_2(n-\tau)d\tau$
• 离散形式：$(f_1*f_2)(n) = \sum\limits_{\tau=-\infty}^{\infty}f_1(\tau)f_2(n-\tau)$

形象的解释就是把函数$g$进行翻转，把函数$g$沿着数轴从右边对折，到了左边，也就是“卷”的由来。然后把函数沿着自变量方向平移$n$，再对两个函数的对应元素相乘，再求和，这就是“积”的由来。

2.2. 函数卷积的傅里叶变换

传统傅里叶卷积：函数卷积的傅里叶变换是函数傅里叶变换的乘积；或者说函数卷积是函数傅里叶变化乘积的逆变换。

设两个时域信号$f_1(t), f_2(t)$，它们卷积的傅里叶变换为$f_1(t)*f_2(t)=\int_{-\infty}^\infty f_1(\tau)f_2(t-\tau)d\tau$，下面证明卷积的傅里叶变换是傅里叶变换的乘积：

$$\begin{array}{rl} \text{Fourier}(f_1(t)*f_2(t))&=\int_{-\infty}^\infty[\int_{-\infty}^\infty f_1(\tau)f_2(t-\tau)d\tau]e^{-iwt}dt\\ &=\int_{-\infty}^\infty f_1(\tau)e^{-iw\tau}d\tau \int_{-\infty}^\infty f_2(t-\tau)e^{-iw(t-\tau)}d(t-r)\\ &=g_1(w)g_2(w)\\ f_1(t)*f_2(t) &= \text{Inverse_Fourier}(g_1(w)g_2(w))\\ &=\frac{1}{2\pi}\int g_1(w)g_2(w)e^{iwt}dw \end{array}$$

2.3. 图卷积

[3-1] If you are familiar with CNN, ‘convolution’ in GCNs is basically the same operation. It refers to multiplying the input neurons with a set of weights that are commonly known as filters or kernels.

Within the same layer, the same filter will be used throughout image, this is referred to as weight sharing.

图的卷积需要类比传统卷积公式并结合傅里叶变换来定义：两个图信号的卷积是图信号傅里叶变换乘积的逆变换。

假设图信号$f$的傅里叶变换为$g=U^Tf$，卷积核（另一个图信号）$h$的傅里叶变换定义为一个对角矩阵

$$\begin{pmatrix} \hat{h}(\lambda_1)&&\\ &\ddots&\\ &&\hat{h}(\lambda_n) \end{pmatrix}$$

其中$\hat{h}(\lambda_l) = \sum\limits_{i=1}^nh(i)u^*_l(i)$，是根据需要设计出来的卷积核$h$在图上的傅里叶变换，其实我们只在乎傅里叶变换之后的矩阵，不在乎原来的卷积核$h$长什么样子。

这两个傅里叶变换的乘积为（这里的$U$与上一章的$U$相同）

$$\begin{pmatrix} \hat{h}(\lambda_1)&&\\ &\ddots&\\ &&\hat{h}(\lambda_n) \end{pmatrix} U^Tf$$

最后的，参考图傅里叶逆变换，这个乘积的逆变换为（重要！）

$$(f*h)_G=U \begin{pmatrix} \hat{h}(\lambda_1)&&\\ &\ddots&\\ &&\hat{h}(\lambda_n) \end{pmatrix} U^Tf$$

以上即为图卷积的公式，也可以写作$(f*h)_G=U((U^Th)\odot(U^Tf))$，其中$\odot$表示Hadamard product，是逐元素乘积运算，这篇文章证明了以上两个公式是等价的。

3. 深度学习中的图卷积

CNN中的卷积核是可训练的、参数共享的kernel，在图神经网络中也是一样的目的。结合上面图卷积的结论，这个共享的卷积参数就是对角矩阵$\text{diag}(\hat{h}(\lambda_l))$.

我们只讨论一层图卷积神经网络的结构$y_=\sigma(U\cdot\text{diag}(\hat{h}(\lambda_l)\cdot U^Tx)$，其中$x$是图信号（每个顶点的feature vector），$\sigma$是激活函数，$y$是经过这层图卷积网络的输出。

3.1. GCN v1

把卷积核$\text{diag}(\hat{h}(\lambda_l))$简化为$\text{diag}(\theta_l)$（或者记为$g_{\theta}(\Lambda)$），这样$y_=\sigma(U\cdot g_{\theta}(\Lambda)\cdot U^Tx)$，其中

$$g_{\theta}(\Lambda)= \begin{pmatrix} \theta_1&&\\ &\ddots&\\ &&\theta_n \end{pmatrix}$$

矩阵中的元素$(\theta_1,\theta_2,\dots,\theta_n)$就是神经网络里面的weights参数，用来训练。

也可以把特征向量矩阵与$\Lambda$参数放在一起考虑，这时$Ug_{\theta}(\Lambda)Ux=g_{\theta}(U^T\Lambda U)x=g_{\theta}(L)x$

这种GCN的缺点：

• 卷积核需要n个参数
• 每一次前向传播都需要计算$(U\cdot\text{diag}(\hat{h}(\lambda_l)\cdot U^T)$三个矩阵乘积，时间复杂度太高
• 这种卷积核不具有Spatial localization

3.2. GCN v2

基于v1的几个缺点进行改进，出现了第二代卷积核。（令上图中的$g_{\theta}(L)=\sum\limits_{j=0}^K\alpha_jL^j$）

把卷积核$\text{diag}(\hat{h}(\lambda_l))$的每一项设为$\sum\limits_{j=0}^K\alpha_j\lambda_l^j$，则

$$g_{\theta}(\Lambda)= \begin{pmatrix} \sum\limits_{j=0}^K\alpha_j\lambda_1^j&&\\ &\ddots&\\ &&\sum\limits_{j=0}^K\alpha_j\lambda_n^j \end{pmatrix}$$

把上面的这个定义写成矩阵符号

$$\begin{array}{rl} \begin{pmatrix} \sum\limits_{j=0}^K\alpha_j\lambda_1^j&&\\ &\ddots&\\ &&\sum\limits_{j=0}^K\alpha_j\lambda_n^j \end{pmatrix}=& \begin{pmatrix} \alpha_0\lambda_1^0&&\\ &\ddots&\\ &&\alpha_0\lambda_n^0 \end{pmatrix}+\dots+ \begin{pmatrix} \alpha_K\lambda_1^K&&\\ &\ddots&\\ &&\alpha_K\lambda_n^K \end{pmatrix}\\ =& \sum\limits_{j=0}^K\alpha_j \begin{pmatrix} \lambda_1^j&&\\ &\ddots&\\ &&\lambda_n^j \end{pmatrix}=\sum\limits_{j=0}^K\alpha_j\Lambda^j \end{array}$$

将这个表达式带入到矩阵乘法的式子

$$\begin{array}{rl} U\sum\limits_{j=0}^K\alpha_j\Lambda_jU^T =& \sum\limits_{j=0}^K\alpha_jU\Lambda^jU^T\\ & (U^TU=I)\\ =& \sum\limits_{j=0}^K\alpha_j\underbrace{(U\Lambda U^T) (U\Lambda U^T) (U\Lambda U^T)}_{\text{j times}}\\ =& \sum\limits_{j=0}^K\alpha_j(U\Lambda U^T)^j\\ =& \sum\limits_{j=0}^K\alpha_jL^j \end{array}$$

由之前文章中拉普拉斯矩阵特征分解的定义，这里的$L$就是拉普拉斯矩阵。这样的话，该层图卷积的输出可以写为

$$y=\sigma(\sum\limits_{j=0}^K\alpha_jL^jx)$$

3.2.1. 为什么要规定上限K

如果设$K=\infty$，则这样的卷积运算会找到这个顶点无限远的邻居点，就是所有顶点，失去了localize卷积的意义。因此需要设置一个上限$K<<n$，称为K-localized。所以令$g_{\theta}(L)=\cos L$或$\sin L$是不合理的，因为三角函数会泰勒展开为无穷多级数的和。

这样设计卷积核改进了上一节提到的三个缺点：

• 卷积核只有K+1个参数$(\alpha_0,\alpha_1,\dots,\alpha_K)$，一般K远小于顶点数$n$.
• 不需要再对拉普拉斯矩阵做特征分解了！直接带入$L$计算即可。但由于要计算$L^j$，时间复杂度$O(N^2)$没有降低。
• 卷积核具备了Spatial localization，即可以用该顶点周围的点的feature更新该顶点的feature。例如K=1是对每个顶点上的一阶邻居点的feature加权求和；K=2对每个顶点上的二阶邻居点的feature加权求和，等等（下一节Local connectivity有例子）。

3.3. GCN v3 (ChebNet)

GCN v3是对GCN v2的改进，因为GCN v2的时间复杂度依然是$O(N^2)$，ChebNet是使用Chebshev多项式来降低时间复杂度。

Chebshev Polynomial：(recursive)

$T_0(x)=1$，$T_1(x)=x$，$T_k(x)=2xT_{k-1}(x)-T_{k-2}(x)$，$x\in[-1,1]$.

把卷积核的参数$\Lambda$代入Chebshev多项式中。首先定义$\widetilde\Lambda=\frac{2\Lambda}{\lambda_{\max}}-I$，（$\widetilde L=\frac{2L}{\lambda_{\max}}-I$），这样$\widetilde\Lambda$的每个元素$\widetilde\lambda$都在$[-1,1]$区间。然后把$\widetilde\Lambda$代入Chebshev多项式：

$$T_o(\widetilde\Lambda)=I, T_1(\widetilde\Lambda)=\widetilde\Lambda, T_k(\widetilde\Lambda)=2\widetilde\Lambda T_{k-1}(\widetilde\Lambda)-T_{k-2}(\widetilde\Lambda)$$

然后用Chebshev多项式重新改写原来的$\Lambda$的多项式函数：

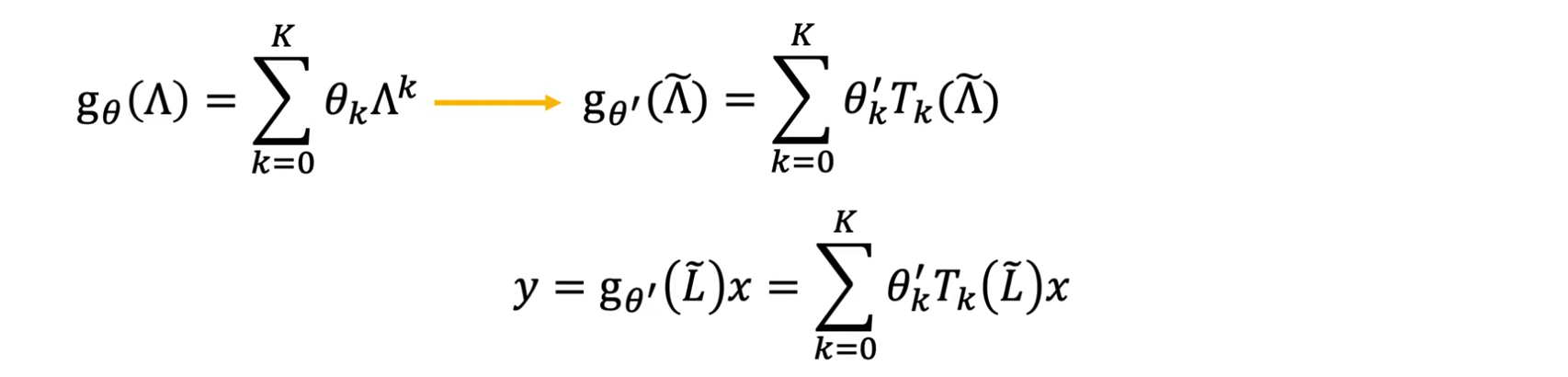
这样做的目的是计算更加容易，怎么做得到呢：（本节没不考虑激活函数$\sigma$）

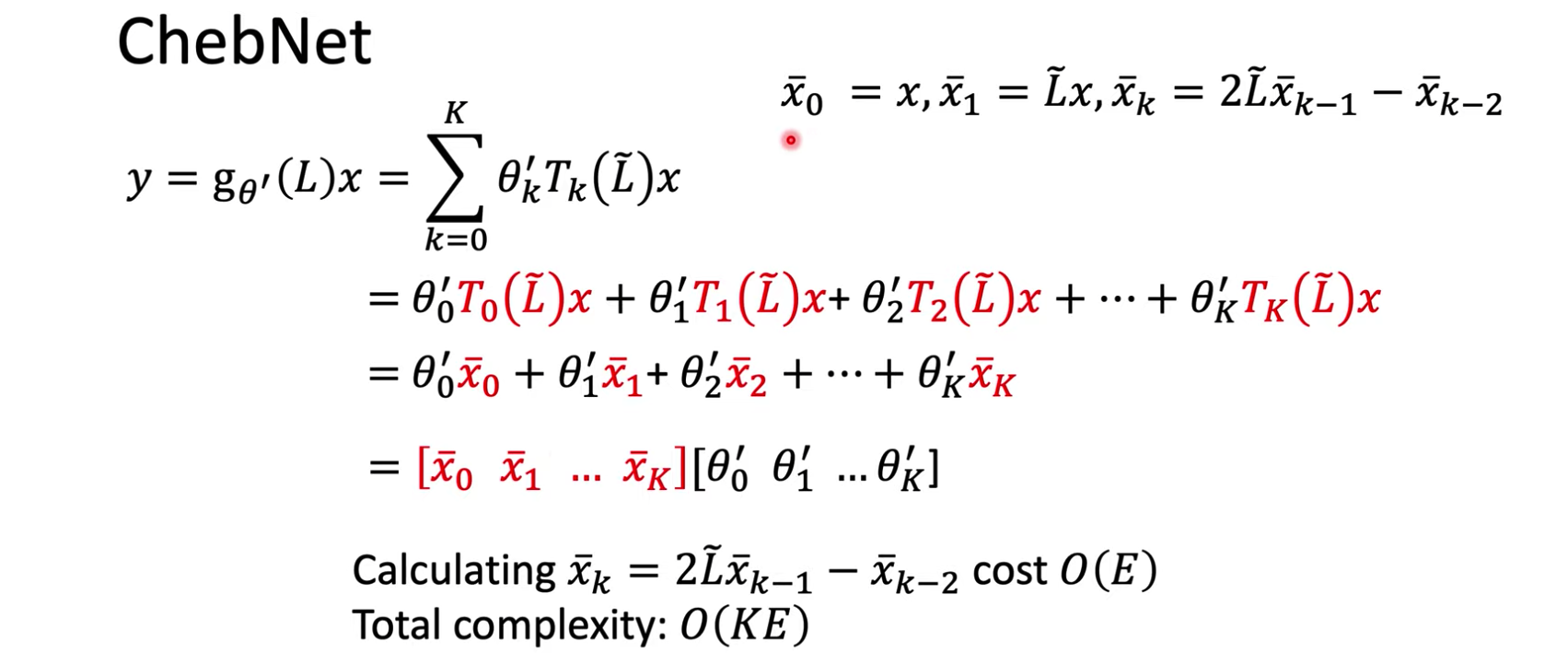
结论就是，用ChebNet我们先将信号按照Chebshev多项式的方式变换得到$[\bar x_0,\bar x_1,\dots,\bar x_K]$，然后训练得到一个参数为$[\theta_0’,\theta_1’,\dots,\theta_K’]$的卷积核。

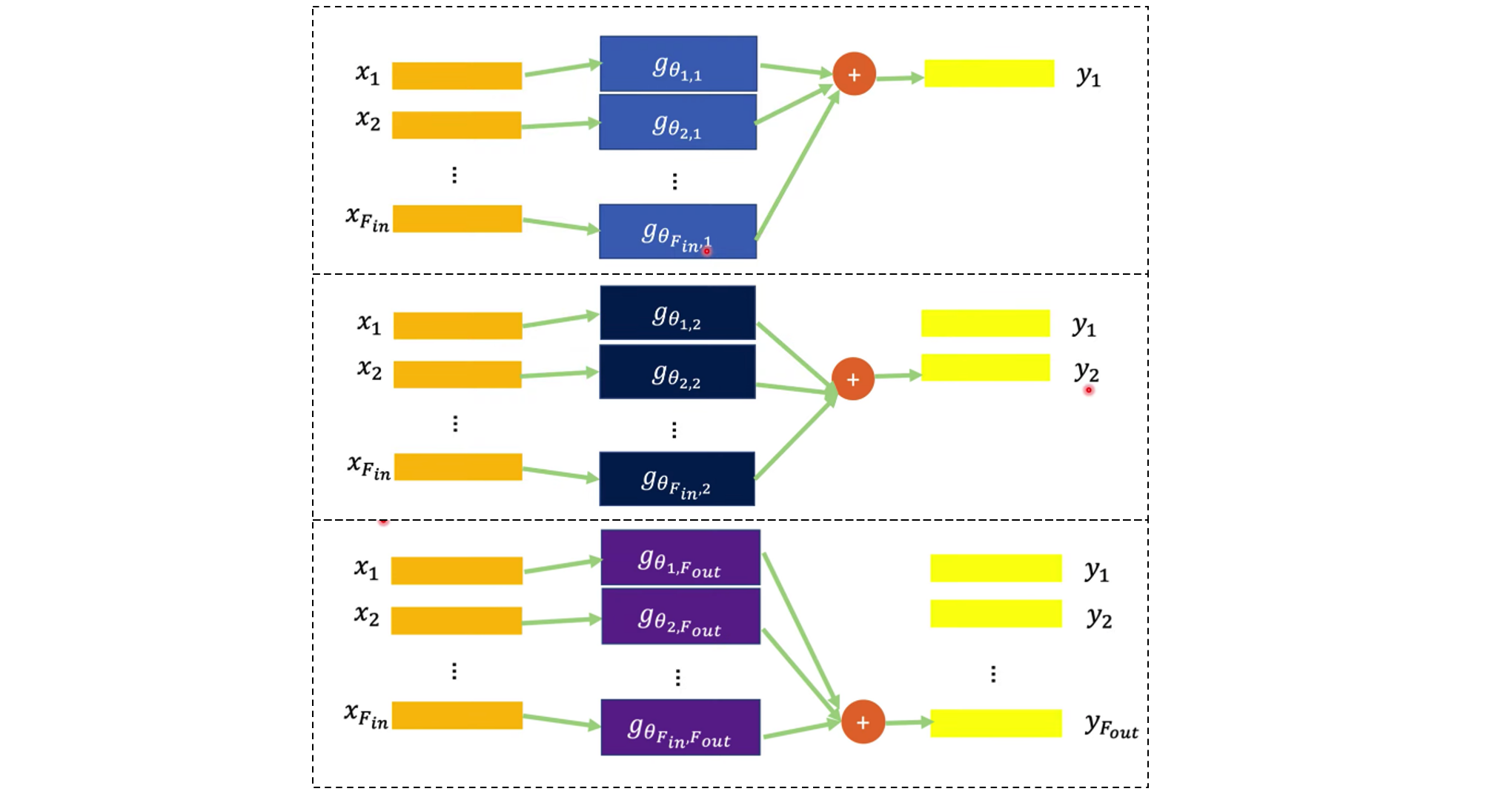
实际上是同时训练多个卷积核，每一个卷积核都要学习参数$[\theta_0’,\theta_1’,\dots,\theta_K’]$，下图指的是$K=F_{\text{in}}$，同时训练$F_{\text{out}}$个卷积核。每个卷积核最后有一个“加法”运算，导致每个卷积核的输出y是一维向量。

3.4. GCN本尊（Kipf et al.）

ChebNet是K-localized的$y=g_{\theta’}(L)x=\sum\limits_{j=0}^K\theta_j’T_j(\widetilde L)x$，如果令$K=1$，就是我们常说的GCN了。

因为$K=1$，这很大程度上简化了ChebNet：（同上节，本节也没不考虑激活函数$\sigma$）

回顾$\widetilde L=\frac{2L}{\lambda_{\max}}-I$；另外在GCN中令拉普拉斯矩阵为normalized矩阵$L=I-D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$，这个矩阵有一个特点是$\lambda_{\max}\approx 2$；最后再令参数$\theta_0’=-\theta_1’=\theta$，使得参数更加简化。由以上这几个tip可推出：

$$\begin{array}{rlll} y=& g_{\theta'}(\widetilde L)x=\theta_0'x+\theta_1'\widetilde Lx &~~~&∵\widetilde L=\frac{2L}{\lambda_{\max}}-I\\ =& \theta_0'x+\theta_1'(\frac{2L}{\lambda_{\max}}-I)x & & ∵\lambda_{\max}\approx2\\ =& \theta_0'x+\theta_1'(L-I)x & & ∵L=I-D^{-\frac{1}{2}}AD^{-\frac{1}{2}}\\ =& \theta_0'x-\theta_1'(D^{-\frac{1}{2}}AD^{-\frac{1}{2}})x & & ∵\theta:=\theta_0'=-\theta_1'\\ =& \theta(I+D^{-\frac{1}{2}}AD^{-\frac{1}{2}})x & & \end{array}$$

再经过一个re-normalization trick：$I_N+D^{-\frac{1}{2}}AD^{-\frac{1}{2}}\rightarrow \widetilde D^{-\frac{1}{2}}\widetilde A\widetilde D^{-\frac{1}{2}}$，这个是作者自己定义的trick。$\widetilde A=A+I$，相当于给邻接矩阵加上selp-loop。经过re-normalization trick，

$$y=\theta(\widetilde D^{-\frac{1}{2}}\widetilde A\widetilde D^{-\frac{1}{2}})x\\ \bbox[yellow]{ \text{i.e.}~~H^{l+1} = \sigma(\widetilde D^{-\frac{1}{2}}\widetilde A\widetilde D^{-\frac{1}{2}}H^{l}W^{l}) }$$

第二个式子的$H^{(l)}$对应第一个式子的$x$；$W^{(l)}$对应$\theta$.

写成最通俗易懂的形式：

$$\bbox[yellow]{ h_v=f(\frac{1}{|\mathcal{N}(v)|}\sum_{u\in\mathcal{N}(v)}Wx_u+b),~~\forall v\in \mathcal{V} }$$

即把顶点v包括自身在内的所有邻居$x_u$的feature经过一系列变换，再乘以参数W，加起来，取平均，加上bias，最后经过激活函数就是输出。搞了这么一大堆推导，结果就是一阶邻居取平均，如此的简单直观。。。

4. 卷积核的特点

CNN中卷积核的特点是：网络局部连接、卷积核参数共享。类似的，图卷积网络的卷积核应该具有同样的特点。

4.1. Local connectivity

Local connectivity不仅要保证相邻的顶点信号能够通过卷积运算后是connected，还要保证不要达到所有顶点都互相影响的程度。设想CNN的kernel大小会控制为3x3，5x5等等，但不会把kernel设成跟image size一样大小。

4.1.1. GCN v1

粗暴的将卷积核设计为$g_{\theta}(\Lambda)$会使得卷积运算是global connectivity，而不是local的。因为卷积运算矩阵$Ug_{\theta}(\Lambda)U^T$的每个元素一般都是非0的，这就意味着在$Ug_{\theta}(\Lambda)U^Tx$的时候，每个顶点的输出值会与所有顶点的feature都有关系。例如下图

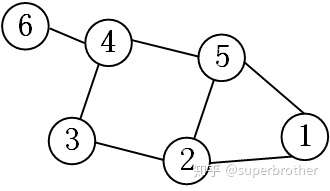
顶点1仅与顶点2和5相邻，如果只考虑一阶邻居，这个6x6的卷积矩阵的第一行应该只有第1、2、5项是非0的，其余都为0. 显然GCN v1做不到local connectivity。

4.1.2. GCN v2

上面这个例子的拉普拉斯矩阵为（最普通的形式$L=D-A$）

$$\begin{pmatrix} 2 & -1 & 0 & 0 & -1 & 0\\ -1 & 3 & -1 & 0 & -1 & 0\\ 0 & -1 & 2 & -1 & 0 & 0\\ 0 & 0 & -1 & 3 & -1 & -1\\ -1 & -1 & 0 & -1 & 3 & 0\\ 0 & 0 & 0 & -1 & 0 & 1 \end{pmatrix}$$

$K=0$时卷积运算矩阵为

$$\alpha_0L^0= \begin{pmatrix} \alpha_0 & 0 & 0 & 0 & 0 & 0\\ 0 & \alpha_0 & 0 & 0 & 0 & 0\\ 0 & 0 & \alpha_0 & 0 & 0 & 0\\ 0 & 0 & 0 & \alpha_0 & 0 & 0\\ 0 & 0 & 0 & 0 & \alpha_0 & 0\\ 0 & 0 & 0 & 0 & 0 & \alpha_0\\ \end{pmatrix}$$

$K=1$时卷积运算矩阵为

$$\alpha_0L^0+\alpha_1L^1= \begin{pmatrix} \alpha_0+2\alpha_1 & -\alpha_1 & 0 & 0 & -\alpha_1 & 0\\ -\alpha_1 & \alpha_0+3\alpha_1 & -\alpha_1 & 0 & -\alpha_1 & 0\\ 0 & -\alpha_1 & \alpha_0+2\alpha_1 & -\alpha_1 & 0 & 0\\ 0 & 0 & -\alpha_1 & \alpha_0+3\alpha_1 & -\alpha_1 & -\alpha_1\\ -\alpha_1 & -\alpha_1 & 0 & -\alpha_1 & \alpha_0+3\alpha_1 & 0\\ 0 & 0 & 0 & -\alpha_1 & 0 & \alpha_0+\alpha_1\\ \end{pmatrix}$$

$K=2$时卷积运算矩阵为

$$\alpha_0L^0+\alpha_1L^1+\alpha_2L^2= \begin{pmatrix} \alpha_0+2\alpha_1+6\alpha_2 & -\alpha_1-4\alpha_2 & \alpha_2 & \alpha_2 & -\alpha_1-4\alpha_2 & 0\\ -\alpha_1-4\alpha_2 & \alpha_0+3\alpha_1+12\alpha_2 & -\alpha_1-5\alpha_2 & 2\alpha_2 & -\alpha_1-5\alpha_2 & 0\\ \alpha_2 & -\alpha_1-5\alpha_2 & \alpha_0+2\alpha_1+6\alpha_2 & -\alpha_1-5\alpha_2 & 2\alpha_2 & \alpha_2\\ \alpha_2 & 2\alpha_2 & -\alpha_1-5\alpha_2 & \alpha_0+3\alpha_1+12\alpha_2 & -\alpha_1-6\alpha_2 & -\alpha_1-4\alpha_2\\ -\alpha_1-4\alpha_2 & -\alpha_1-5\alpha_2 & 2\alpha_2 & -\alpha_1-6\alpha_2 & \alpha_0+3\alpha_1+12\alpha_2 & \alpha_2\\ 0 & 0 & \alpha_2 & -\alpha_1-4\alpha_2 & \alpha_2 & \alpha_0+\alpha_1+2\alpha_2\\ \end{pmatrix}$$

GCN v2的卷积运算矩阵就具备local connectivity的特点，当$K=1$时每个点（矩阵的每一行）只有一阶邻居元素值非0，$K=2$时每个点只有二阶邻居元素值非0。

4.2. Parameter sharing

4.2.1. GCN v2

GCN v2的参数共享，可以由上面的例子来解释：当$K=0$，只有一个参数$\alpha_0$，即所有顶点自身的特征由共享的$\alpha_0$控制，更高阶的邻居点没有参与；$K=1$时，一阶邻居点的卷积由共享的$\alpha_1$控制；$K=2$时，二阶邻居点的卷积由共享的$\alpha_2$控制，等等。

• 优点：可以实现越远的点，相关性越低。（找到一组参数满足K越大，$\alpha$越小）这样具备一定的物理意义。
• 缺点：只有K个参数，太少，使得模型无法很好的实现在同阶的邻域上分配不同的权重给不同的邻居。（GAT论文里说的 enable specifying different weights to different nodes in a neighborhood）

4.2.2. GCN本尊（Kipf et al. [3-2]）

这里GCN的输出为$H^{l+1}=\sigma(D^{-\frac{1}{2}}\widetilde{A}D^{-\frac{1}{2}}H^lW^l)$，其中$D$是degree matrix，$\widetilde{A}=A+I$是邻接矩阵加上self loop，$H^l$是上一层的输出，$W^l$是参数。$\widetilde{A}$给邻接矩阵加了self loop，所以顶点会同时考虑自身的feature。$D^{-\frac{1}{2}}\widetilde{A}D^{-\frac{1}{2}}$是$D^{-1}\hat{A}$的改进版，目的都是对$\widetilde{A}$归一化，使得$(D^{-\frac{1}{2}}\widetilde{A}D^{-\frac{1}{2}})H^l$数值的scale不变。（这种GCN只能聚合一阶邻居点的信息，要通过堆GCN的层数来实现多阶邻居信息的聚合。）

• 优点：为什么$W^l$放在最后面？这样$W^l$的维度与顶点数和顶点的度都没有关系，这个超参数可以任意调节。因为$W^l$的选取不需要考虑顶点数和顶点的度，所以不care训练数据和测试数据的结构是否一致。
• 缺点：无法很好的实现同阶的邻域上分配不同的权重给不同的邻居（缺点与GCN v2相同）

5. Reference

• 如何理解 Graph Convolutional Network（GCN）？ （重点参考）
• 李宏毅助教 Graph Neural Network - Youtube

1. Graph Fourier Transform
   • Wiki: Graph Fourier Transform
   • 图卷积神经网络系列：2. | 图傅里叶变换
   • 图上的傅里叶变换和逆变换（重点参考）
2. 图卷积
   • 如何通俗易懂地解释卷积？
   • 从传统傅里叶变换到图卷积
3. GCN
   1. Understanding Graph Convolutional Networks for Node Classification （很有参考价值）
   2. Graph Convolutional Networks （经典博客）